our main character: o, ω, O, Ω and Θ
DEFINITION
Asymptotic Notation
: Asymptotic notations are the mathematical notations used to describe the running time of an algorithm when the input tends towards a particular value or a limiting value.
Why we use asymptotic notation instead of detailed run-time function?
- :fire: TRIGGER:
- The function describe algorithm is too complicate to see how an algorithm performs.
- We’re only interested in the broad headlines of how some function behaves。
- :star: MOTIVATION:
- We find it is possible to classify these ‘complicate’ functions via ‘simple’ ones.
- :boom: ATTAMPTS:
- Asymptotic Notation :heavy_check_mark:
- :sparkles: CONSEQUENCE:
- Reduce clutter and simplify calculation.
- Way of making precise, quantitative statements about efficiency properties of algorithms themselves.
How to use asymptotic notation?
There are 5 different asymptotic notation: o, ω, O, Ω and Θ. And they share some PROPERTIES.
- $x(g) = {f : N → R≥0 | {~definition~} {~of~} x}$ , where x is one of these five.
- So,
f is x(g)technically meansf ∈ x(g).
Then let’s see how to use each of them
- Example case
- f = o(g)
- How to say
- f is asymptotically smaller than / grows slower than g
- In the limit, f is vanishingly small relative to g
- Definition
- ∀c > 0. ∃N. ∀n ≥ N. f (n) < cg(n)
- Property
- A robust statement about f and g. E.g. unaffected by scaling: f = o(g) ⇔ 3f = o(0.2g)
- Memory tips
- Little o
- g 在增长级数上碾压 f
- Example case
- f = ω(g)
- How to say
- g is asymptotically larger than / grows faster than f
- Definition
- ∀C > 0. ∃N. ∀n ≥ N. f (n) > Cg(n)
- Property
- A robust statement about f , g. Same as Little o.
- f = o(g) ⇔ g = ω(f )
- Memory tips
- Think ‘C = 1/c’
- Compare: x < y if and only if y > x.
- g 增长级数上永远小于 f
- Example case
- f = O(g)
- How to say
- f is O(g) ‘f grows no faster than g’
- call g an asymptotic upper bound for f
- Definition
- ∃c > 0. ∃N. ∀n ≥ N. f (n) ≤ cg(n)
- Property
- f = o(g) implies f = O(g)
- Notice
- Different with Little o:
- For o we require that any multiple of g eventually overtakes f .
- For O it’s enough that some multiple of g does.
- ∀c compare with ∃C
- If f = O(n^2) is a tight upper bound, f = O(n^3) is true but not a - tight upper bound.
- Different with Little o:
- Memory tips
- Big O
- Loosely, can think of o as like <, O as like ≤.
- g 在增长级数上和 f 类似,但会存在 g 的增长率大于 f 的情况
- Example case
- f = Ω(g)
- How to say
- f is Ω(g) ‘f grows no slower than g’
- g is an asymptotic lower bound for f
- Definition
- ∃C > 0. ∃N. ∀n ≥ N. f (n) ≥ Cg(n)
- Property
- f = O(g) ⇔ g = Ω(f )
- Memory tips
- Ω(g) ≤ Θ(g) ≤ O(g)
- g 在增长级数上和 f 类似,但会存在 g 的增长率小于 f 的情况
- Example case
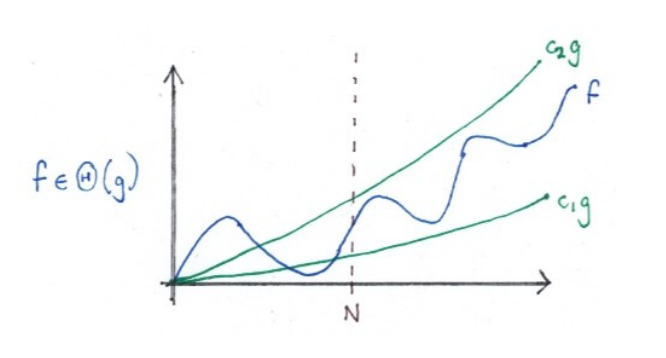
- f = Θ(g)
- How to say
- f and g have ‘essentially the same growth rate’
- g is an asymptotically tight bound for f
- Definition
- ∃c1, c2 > 0. ∃N. ∀n ≥ N. c1g(n) ≤ f (n) ≤ c2g(n)
- Property
- f = Θ(g) ⇔ g = Θ(f )
- f is Θ(g) ⇔ f is O(g) and f is Ω(g)
- Memory tips
Other
- for some runtime function T(n):
- T(n) = O(g) says runtime is not essentially worse than g(n),
- T(n) = Ω(g) says runtime is not essentially better than g(n).
If you have better memory tips, tell my in the comment. It will be great.