注:封面画师:新雨林-触站
说明
- 本页面无手机端适配,强制缩放阅读。
- 使用纯html格式,保存教学用ppt,添加了部分个人笔记。
- 目录工作正常,可以跳转。
反向传播
这里对反向传播的讲解比较奇怪,可能比较适合初学者理解。想要通过严谨的数学推导理解反向传播的同学,可以搜索一下。
反向传播算法
反向传播算法
什么是正向传播网络
什么是反向传播
反向传播算法
为什么需要反向传播
图解反向传播
反向传播计算
链式求导法则
案例1:通过反向传播计算偏导数

知
识
讲
解
什么是正向传播网络
• 前一层的输出作为后一层的输入的逻辑结构,每一层神经元仅与下一层的
神经元全连接,通过增加神经网络的层数虽然可为其提供更大的灵活性,
让网络具有更强的表征能力,也就是说,能解决的问题更多,但随之而来
的
数量庞大的网络参数的训练,一直是制约多层神经网络发展的一个重要
瓶颈。

知
识
讲
解
什么是反向传播
• 反向传播(Backpropagation algorithm)全称“误差反向传播”,是在
深度神经网络中,根据输出层输出值,来反向调整隐藏层权重的一种方法。
知
识
讲
解
为什么需要反向传播
• 为什么不直接使用梯度下降而使用反向传播方式更新权重呢?
• 梯度下降应用于有明确求导函数的情况,或者可以求出误差的情况(比如
线性回归),我们可以把它看做没有隐藏层的网络。
但对于多个隐藏层的
神经网络,输出层可以直接求出误差来更新参数,但隐藏层的误差是不存
在的,因此不能对它直接应用梯度下降,而是先将误差反向传播至隐藏层,
然后再应用梯度下降。
知
识
讲
解
反向传播算法极简史
• 1974年,哈佛大学沃伯斯博士在他的博士论文中,首次提出了
通过误差的反向传播来
训练人工神经网络,以解决神经网络数量庞大的参数训练问题。
但是,沃伯斯的工作
并没有得到足够的重视,因为当时神经网络正陷入低潮,可谓“生不逢时”。
• 1986年,由杰弗里·辛顿(Geoffrey Hinton)和大卫·鲁姆哈特(David Rumelhart)
等人在著名学术期刊Nature(自然)上发表了论文“借助误差反向传播算法的学习表
征(Learning Representations by Back-propagating errors)”,系统而简洁地
阐述了反向传播算法在神经网络模型上的应用。反向传播算法非常好使,它直接把纠
错的运算量降低到只和神经元数目本身成正比的程度。

知
识
讲
解
反向传播算法极简史(续)
• 后来,沃伯斯得到了IEEE(电气电子工程师学会)神经网络分会的先驱奖;Geoffrey
Hinton与Yoshua Bengio、Yann LeCun(合称“深度学习三巨头”)共同获得了
2018年的图灵奖
沃伯斯
杰弗里·辛顿
知
识
讲
解
图解反向传播
• 问题:Tom在超市买了2个苹果,每个10元,消费税10%,请计算应该支付
的金额
×
10
20
×
22
2
苹果个数
1.1
消费税
知
识
讲
解
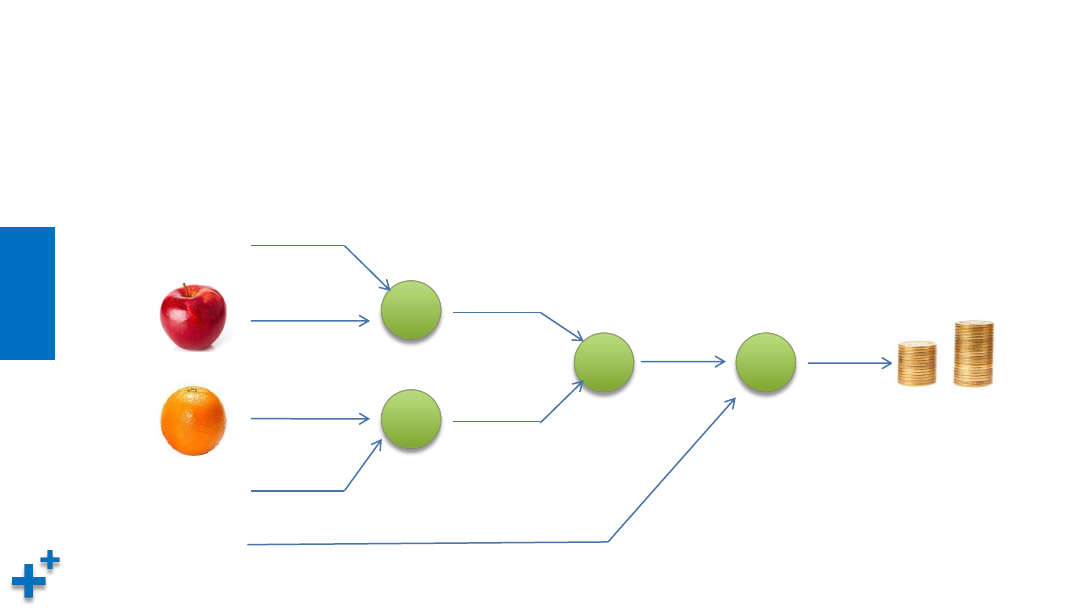
图解反向传播(续1)
• 问题:Tom在超市买了2个苹果,3个橙子,其中苹果每个10元,橙子每个
15元,消费税10%,请计算应该支付的金额
×
10
20
+
65
2
苹果个数
1.1
消费税
15
×
橙子个数
3
45
×
71.5
知
识
讲
解
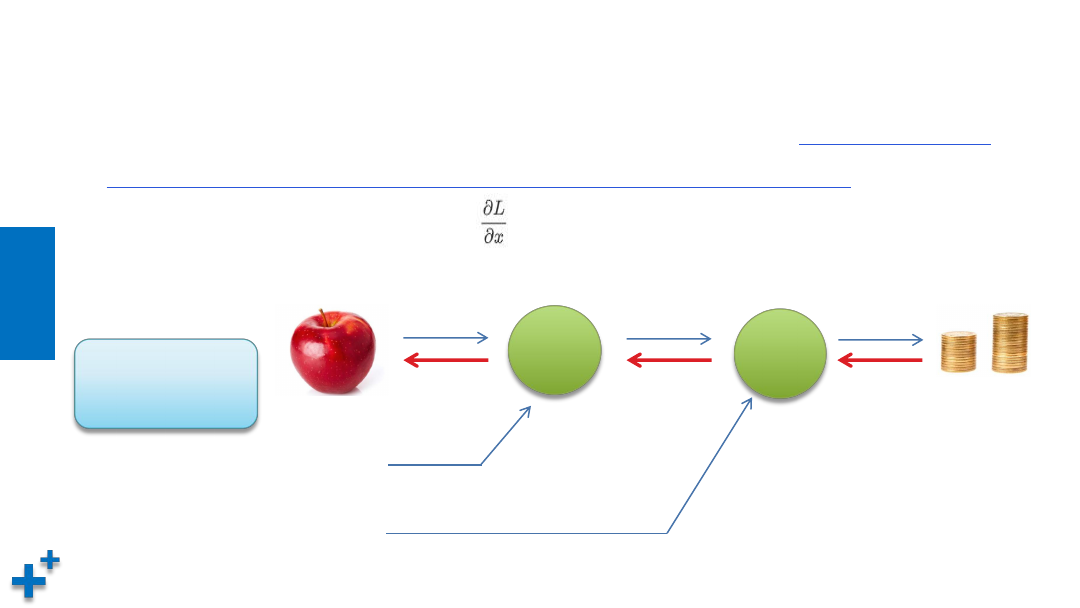
图解反向传播(续2)
• 问题:Tom在超市买了2个苹果,每个10元,消费税10%,请计算
苹果价格上涨会在
多大程度上影响支付金额(即求“支付金额关于苹果的价格的导数”)
。
设苹果的价
格为x,支付金额为L,则相当于求 。这个导数的值表示当苹果的价格稍微上涨
时,支付金额会增加多少。
×
10
20
×
22
2
苹果个数
1.1
消费税
1.1
2.2
1
苹果价格增长1
支付金额增加2.2
知
识
讲
解
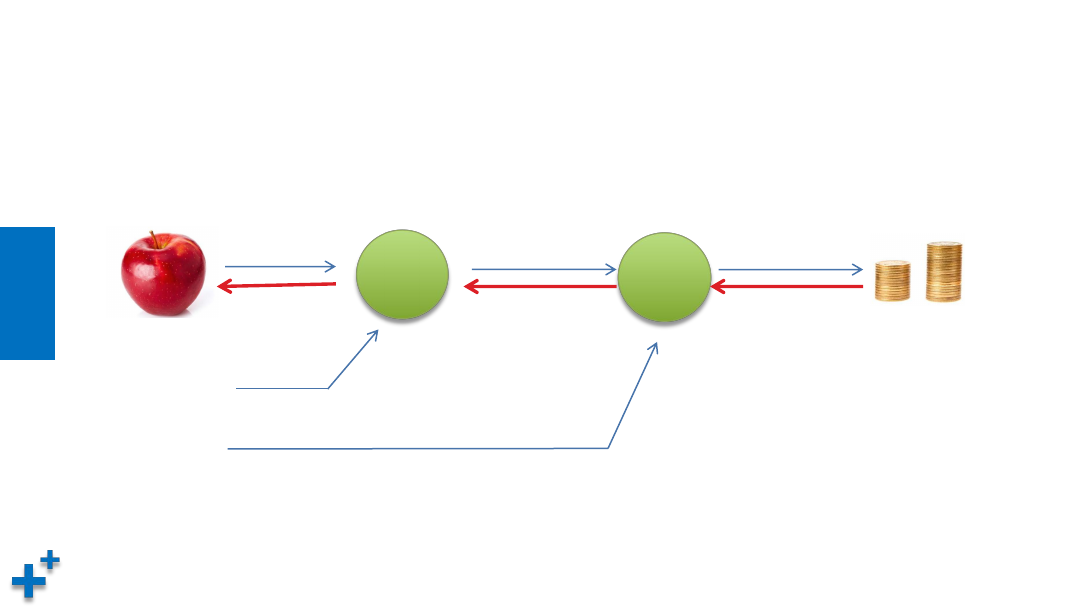
图解反向传播(续3)
×
10
20
×
22
2
苹果个数
1.1
消费税
1.1
2.2
1
21
23.1
11
22
24.2
1.1
2.2
知
识
讲
解
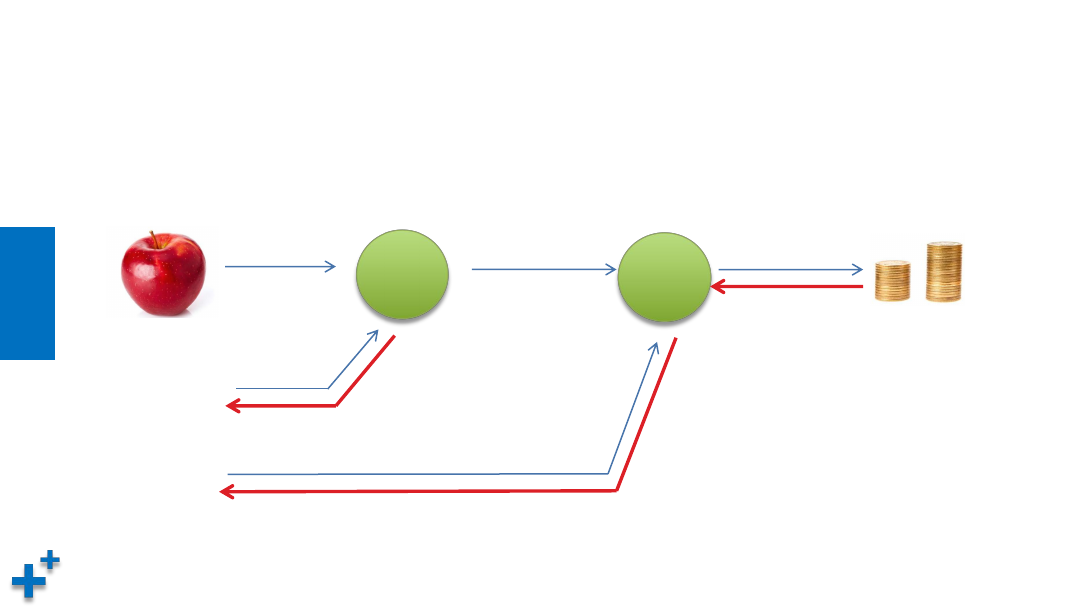
图解反向传播(续4)
×
10
20
×
22
2
苹果个数
1.1
消费税
1
42
30
33
20
11
2.1
3
20
11
知
识
讲
解
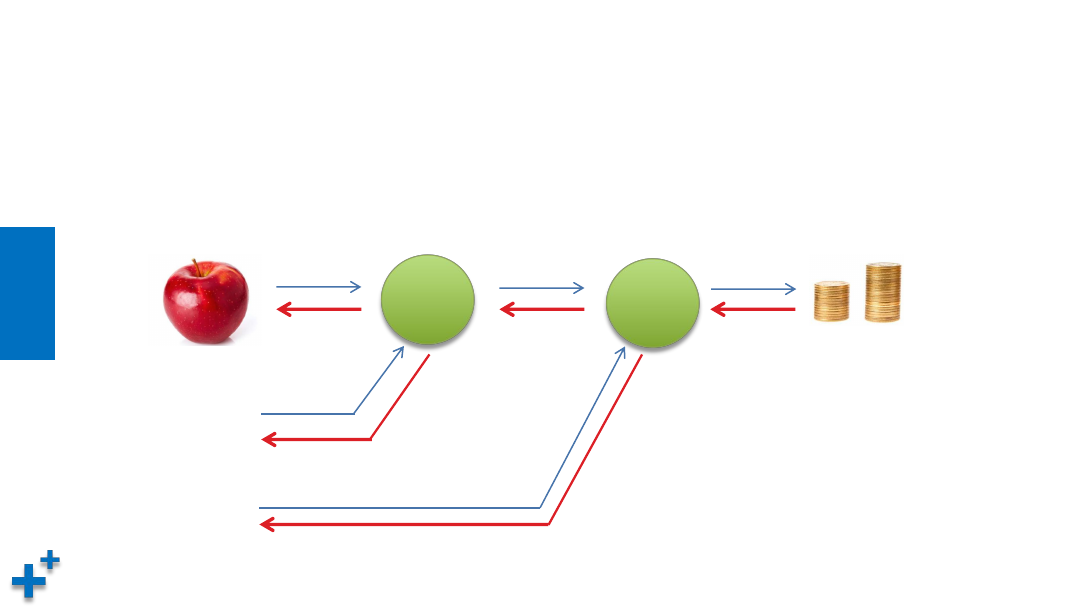
图解反向传播(续5)
苹果价格的导数为2.2,苹果个数导数为11,消费税导数为20,可以解释为:苹果价格、
苹果个数或消费税增加相同的值,分别对支付金额产生2.2倍、11倍、20倍的影响
×
10
20
×
22
2
苹果个数
1.1
消费税
1.1
2.2
1
20
11
知
识
讲
解
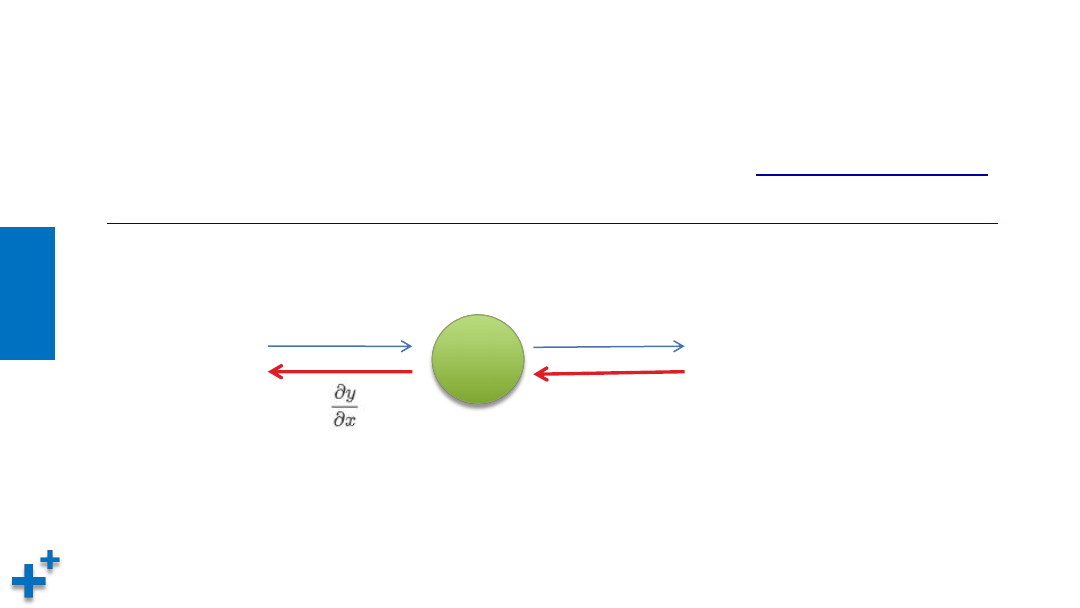
反向传播计算
• 考虑函数
y = f(x) ,
输出为E,反向传播的计算顺序是,
将信号E乘以节点的
局部导数(偏导数),传递给前面的节点,这样可以高效地求出导数的值。
f
x
y
E
E
知
识
讲
解
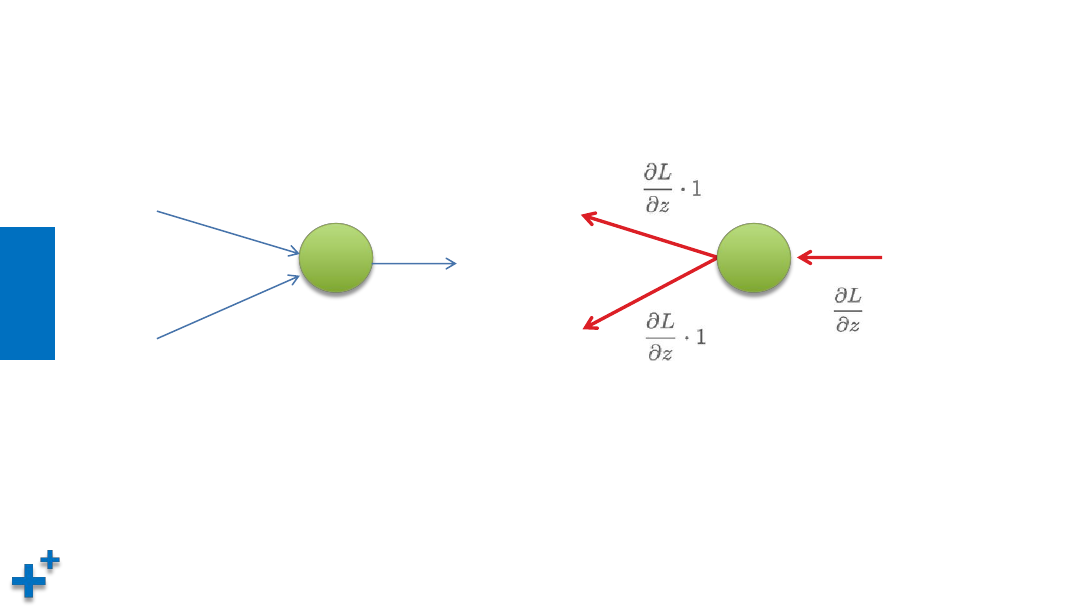
反向传播计算(续1)
• 加法节点反向传播计算
+
x
z
y
+
正向传播
偏导数均为1
反向传播
将上游值原封不动传递给下游
知
识
讲
解
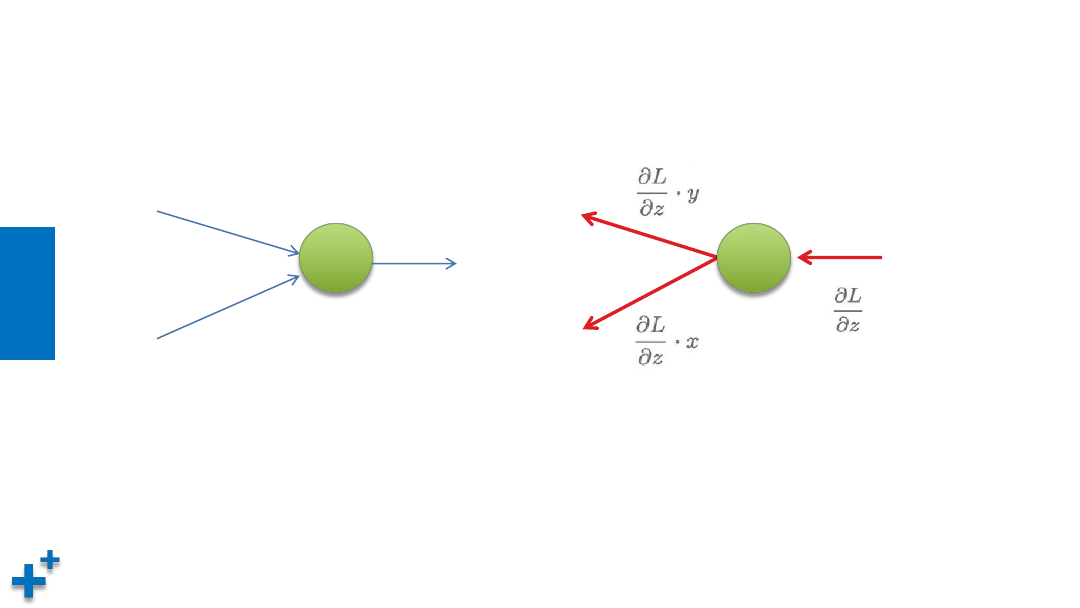
反向传播计算(续2)
• 乘法节点反向传播计算
X
x
z
y
X
正向传播
偏导为x, y
反向传播
将上游信号和正向传播“翻转值”传递给下游
知
识
讲
解
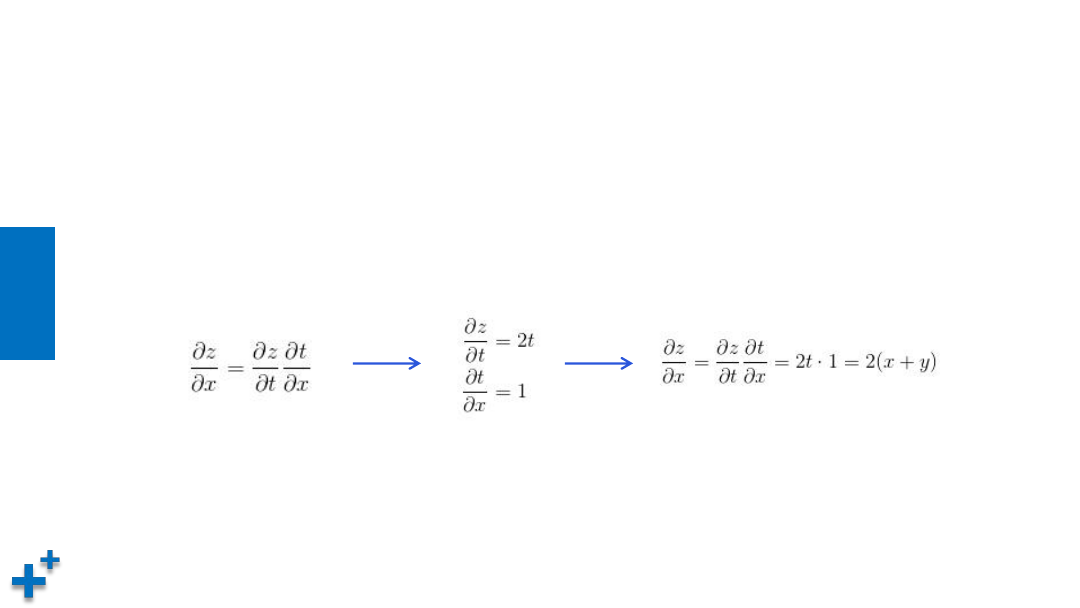
链式求导法则
• 考虑如下复合函数
z = t
2
t = x + y
z
关于
x
的导数(
x
变化对
z
的影响率)可以表示为:
这称之为“链式求导法则”
知
识
讲
解
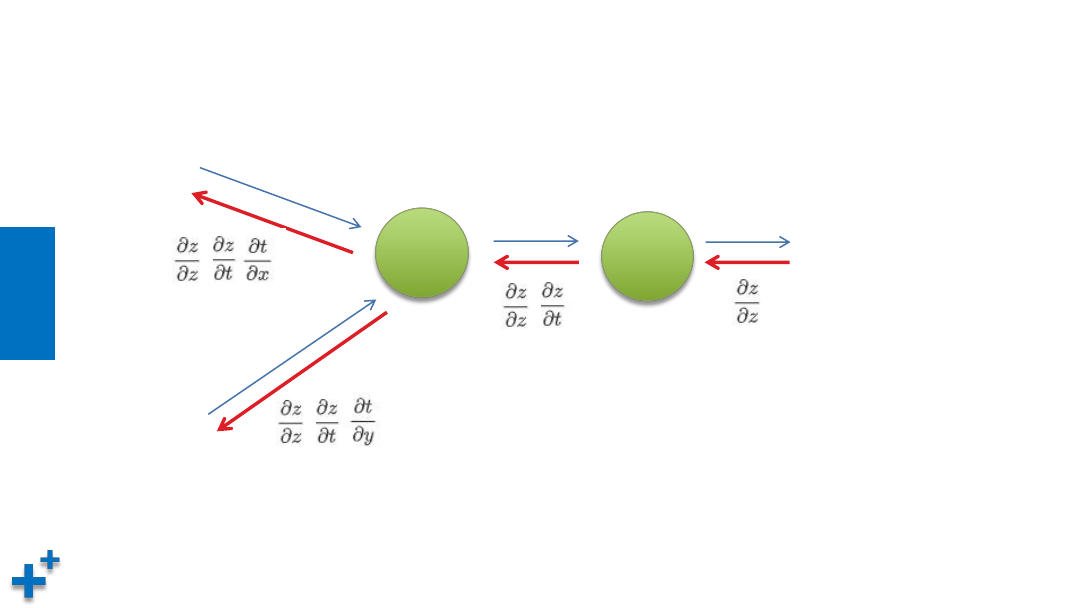
链式求导法则(续)
+
x
t
**2
z
y
知
识
讲
解
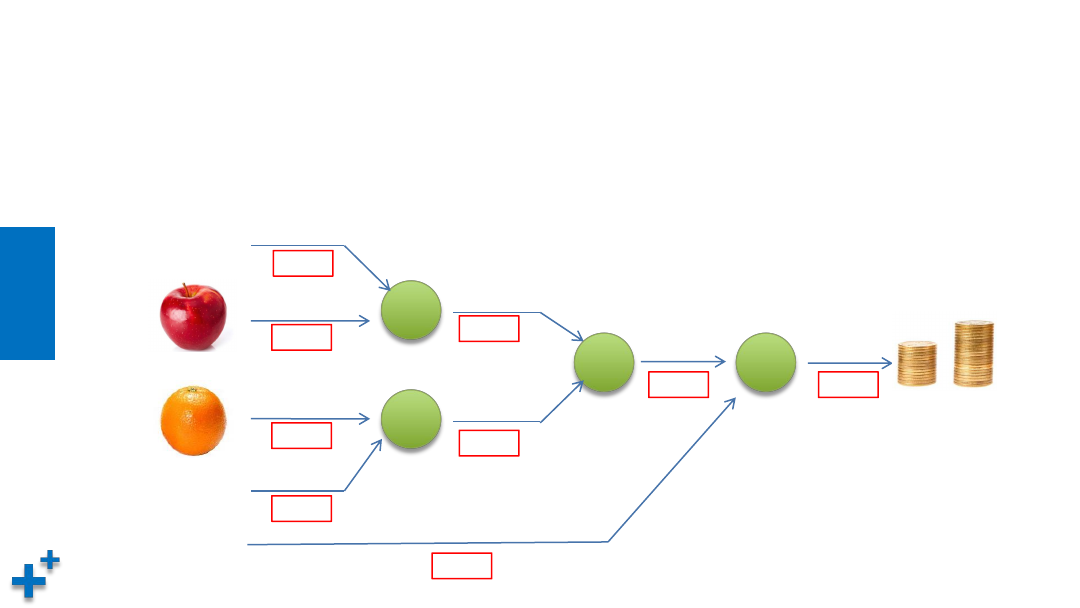
案例1:通过反向传播计算偏导数
• 问题:苹果、橙子价格和个数以及税率如下图所示,利用反向传播算法,在
方框处计算填入导数
×
10
20
+
65
2
苹果个数
1.1
消费税
15
×
橙子个数
3
45
×
71.5
知
识
讲
解
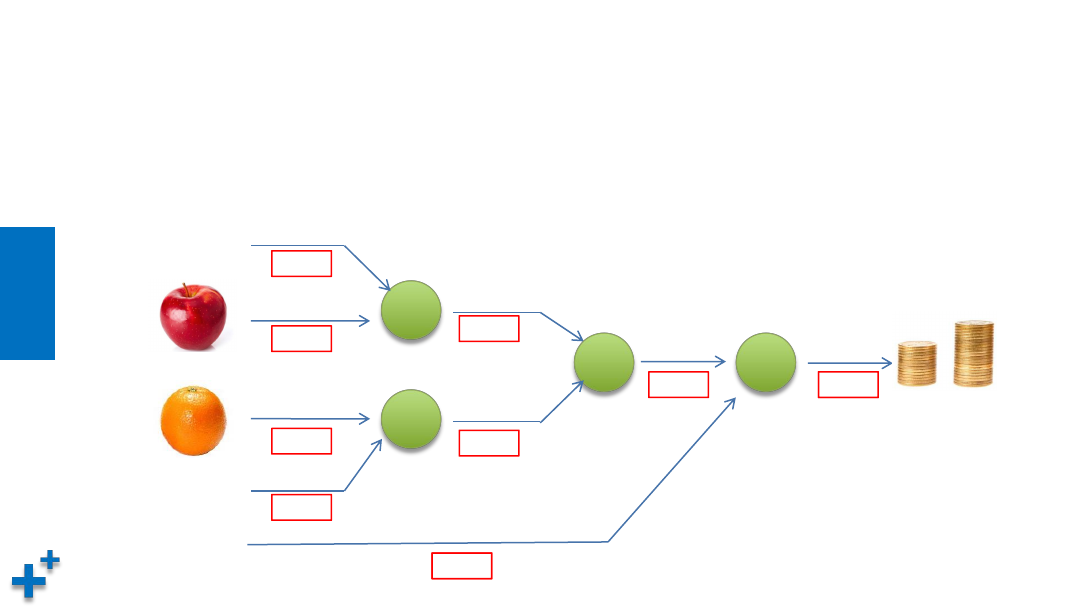
案例1:通过反向传播计算偏导数(续)
• 问题:苹果、橙子价格和个数以及税率如下图所示,利用反向传播算法,在
方框处计算填入导数
×
10
20
+
65
2
苹果个数
1.1
消费税
15
×
橙子个数
3
45
×
71.5
1
1.1
1.1
1.1
65
1
65
16.5
11
2.2
3.3

小结
• 本章节主要介绍了反向传播算法,其目的是根据预测输出,调整权
重参数,使得模型更快收敛。










