【数学】到底什么是拓扑？

目录
@[TOC]

定义

注意：以下内容来自百度百科：拓扑

拓扑（Topology）是研究几何图形或空间在连续改变形状后还能保持不变的一些性质的一个学科。它只考虑物体间的位置关系而不考虑它们的形状和大小。

概念解释

即使这两个对象在几何形状上有所不同，但它们在拓扑上完全等价。我们可以将橡皮泥拉伸成可以想象的任何奇怪形状，但在拓扑结构世界中，所有这些形状都完全相同。也许你对拉伸的形状没有什么概念，但是关于如何拉伸橡皮泥的游戏有一些规则：

不允许在橡皮泥上打洞；
不允许将橡皮泥上的两点捏合在一起（我们没法将球形的橡皮泥做成甜甜圈的形状）。

如果我们在拉伸时违反了这些规则，那么这两个对象在拓扑上将不再等价。拓扑学家称这种不破坏既定规则的拉伸为同胚，这只是一种数学上精确地描述如何让橡皮泥的形状保持相同拓扑性质的方法。因此，如果我们可以得出两个拓扑空间之间的同胚性，则这些空间具有相同的拓扑，这就说到了咖啡杯和甜甜圈动画。

在拓扑上区分三维对象的另一种常用方法是，想象在三维对象上面行走。例如，在球体上行走。假设你从某个点开始，一直绕着球体上的一个大圆圈行走，当你再次到达同一点后，可以沿任一方向旋转90度，然后绕着另一个大圆圈走。在绕球的第二圈中，你将穿越第一条路径。无论你在球面上的哪一点上执行此操作，都会发生这种情况。

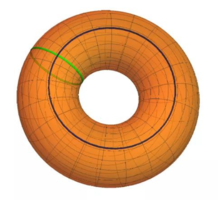
在与球体拓扑等价的任何三维对象上也会发生这种现象。但是，在某些拓扑上与球体不等价的对象上，有方法可以做到这一点而不穿越第一条路径，你可以在甜甜圈上看到这个现象。

对于拓扑等价的对象，他们的许多拓扑性质都是相同的；对于拓扑不等价的对象，这些拓扑性质则不一定相同。这些拓扑性质，就是用于确定两个对象拓扑等价与否的重要工具。

分析拓扑的工具

研究在三维空间中难以可视化的对象（例如克莱因瓶）的拓扑的一种更实用的方法是考虑其粘合图，粘合图通过拉伸和粘合2D形状的边缘的方式，来指导我们如何构造具有特定拓扑的对象。

在考虑复杂形状的粘合图之前，首先考虑一个更简单形状的粘合图，甜甜圈：

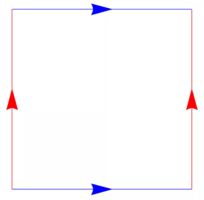
我们假设图中的正方形是用橡皮泥制成的，然后想象一下拉伸正方形让对侧的边缘附着在一起或粘贴起来。当我们将这些边缘粘合在一起时，我们需要箭头指向同一方向。因此，我们将上图扩展如下：

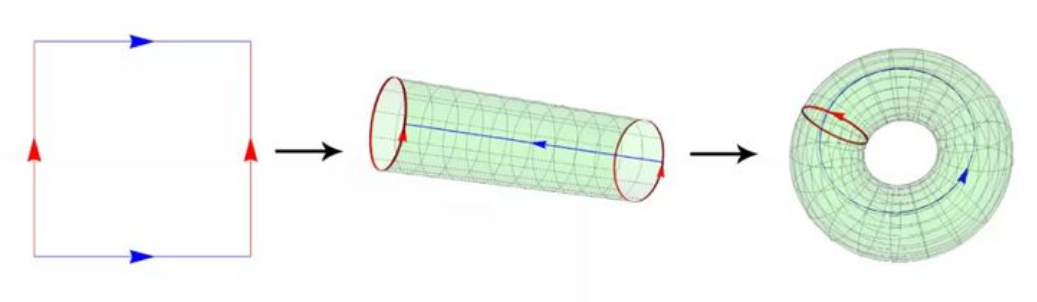
下面这个图像和上图类似，除了两个红色箭头现在处于相反的方向。这意味着我们需要扭曲对象，以便在将边缘胶合在一起之前，箭头指向同一方向：

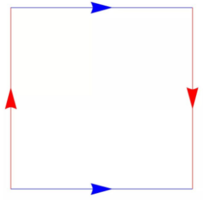
上图粘合图中的第一步是拉伸正方形，使两条蓝线相交，然后我们构造一个圆柱体，就像构建甜甜圈的第一步一样。甜甜圈粘合的红色箭头指向相同的方向，而现在，这两个红色箭头则指向相反的方向。这意味着我们必须以某种方式扭转圆柱体的一端，以使箭头在将它们胶合在一起之前指向相同的方向。你可能会想到，这在物理上是不可能的。因此，由该粘合图产生的表面在物理上也是不可能的。但是实际上，这是我们已经见过的物理上不可能的表面，克莱因瓶！

粘合图是查看对象是否可定向的简单方法。我们可以想象在粘合图上行走与在“吃豆人”中的原理类似，当吃豆人到达世界的一侧时，它可以从另一侧出来。如果我们想象吃豆人在粘合图上移动，当它进入一侧时，它将从同一颜色的另一侧冒出来，而箭头确定了它前进的方向。

假设吃豆人进入圆环粘合图的右侧，那么它将从左侧出现。这就是正常“吃豆人”世界的拓扑工作方式。

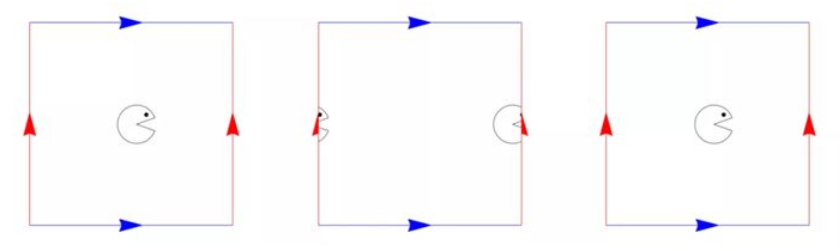
现在假设吃豆人进入了克莱因瓶粘合图的右侧，然后，吃豆人将在左侧出现，但上下颠倒了：

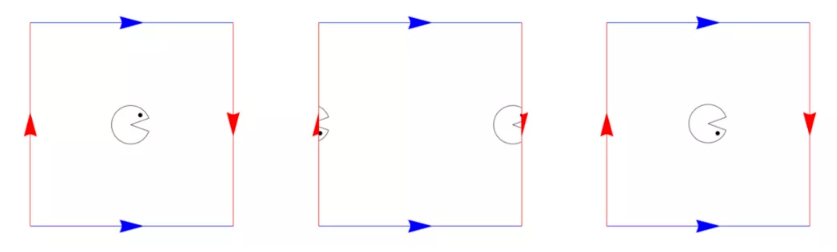
由以上分析可知: 粘合图能使我们轻松考虑对象的某些拓扑属性，如果没有粘合图，这些属性将难以理解和利用。

点集拓扑学

注意：以下内容来自知乎回答：拓扑是什么概念？

数学定义

定义使用

空间拓扑

注意：以下内容来自CSDN：代数拓扑\集合拓扑\代数拓扑\拓扑关系\拓扑结构_笔记

平面拓扑

简而言之，一个空间对象可定义为由内部+边界构成。

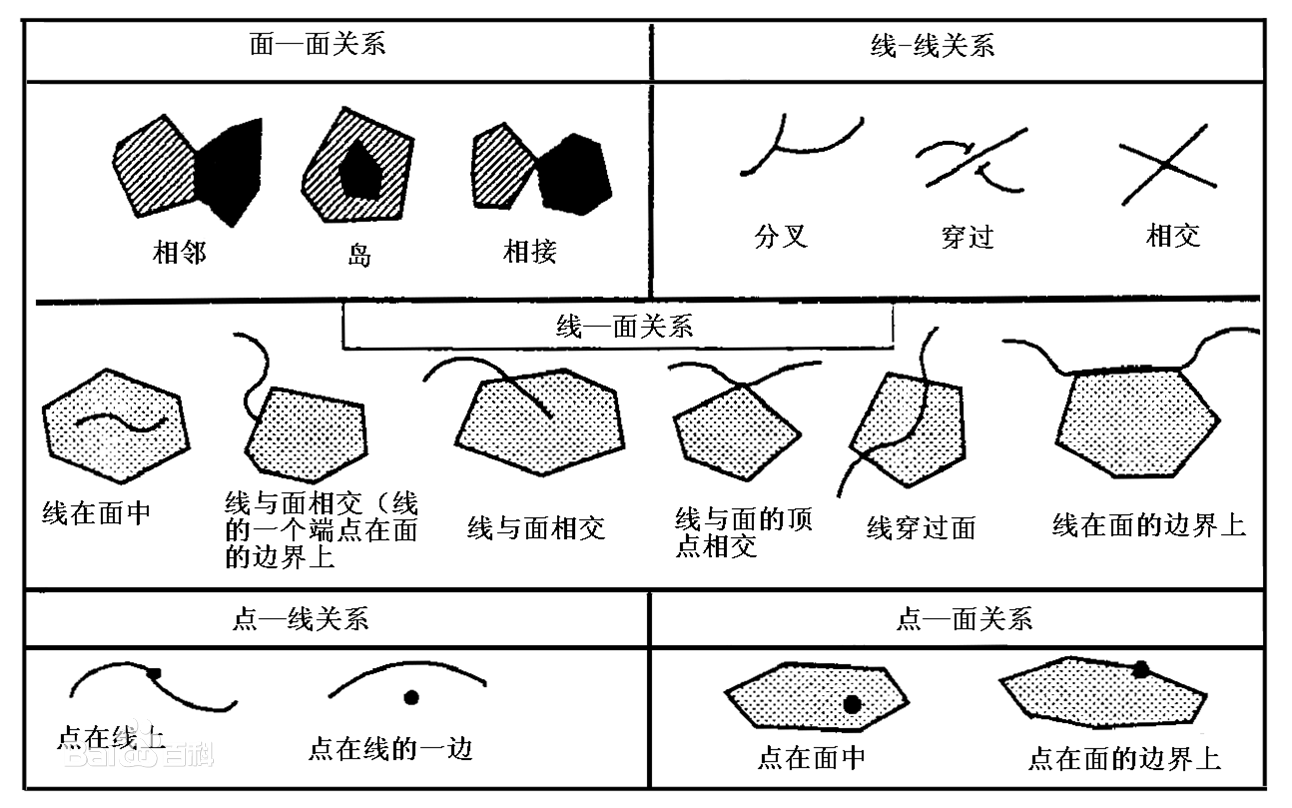
三维空间拓扑关系

点-点空间关系2种：相离、相等；
点-线空间关系3种：相离、相接、包含于；
点-面空间关系3种：相离、相接、包含于；
点-体空间关系3种：相离、相接、包含于；
线-线空间关系7种：相离、相交、交叠、相等、相接、包含于、包含；
线-面空间关系5种：相离、相接、进入、穿越、包含于；
线-体空间关系5种：相离、相接、进入、穿越、包含于；
面-面空间关系10种：相离、相接、交叠、相等、包含于、包含、覆盖、被覆盖、穿越、被穿越；
面-体空间关系8种：相离、相接、交叠、进入、包含于、包含、穿越、被穿越；
体-体空间关系8种：相离、相接、进入、相等、包含于、包含、穿越、被穿越。

拓扑的应用

一种思想

拓扑是一个思想，在网络中，拓扑形象地描述了网络的安排和配置，包括各种结点和结点的相互关系。拓扑不关心事物的细节也不在乎什么相互的比例关系，只将讨论范围内的事物之间的相互关系表示出来，将这些事物之间的关系通过图表示出来。网络中的计算机等设备要实现互联，就需要以一定的结构方式进行连接，这种连接方式就叫做”拓扑结构”，通俗地讲这些网络设备如何连接在一起的。

一种辅助定位的信息

核心提示：几何元素之间由两种重要的信息表示。一是几何信息，另一是拓扑信息。

几何信息

几何信息是指一个物体在三维欧氏空间中的位置信息。它们反映物体的大小和位置，例如顶点的坐标值、曲面数学表达式中的具体系数等。通常用空间直角坐标系表示各种几何数据。

例如，空间一个点可以用它的位置矢量表示，也可以用它在三维直角坐标系中的3个坐标分量定义;对于一条空间直线，则可以用它的两个端点的位置矢量来表示，也可以用端点在三维直角坐标系中的坐标分量定义;对于一个空间平面，可用平面方程表达;对于圆柱面、圆锥面、球而等二次曲面用二次方程表达;自由曲面常采用孔斯曲面、B样条曲面、Bezier曲面等描述。

但是只有几何信息难以准确地表示物体，常会出现物体表示上的二义性，可能产生多个不同的理解。为了确保描述物体的完整性和数学的严密性，必须同时给出几何信息和拓扑信息。

拓扑信息

拓扑信息是指物体的拓扑元素(顶点Vertex、边Edge和表面Face)的个数、类型以及它们之间的相互关系信息。拓扑是研究在形变状态下图形空间性质保持不变的一个数学分支，着重研究图形内的相对位置关系。例如，某一面与哪些面相邻、某一面由哪些点组成等都属于拓扑信息。

表示拓扑信息常用数据结构来实现，采用体、面、环、边和顶点表示，根据这些信息可以确定物体表面的邻接关系。一般，多面体的拓扑元素有9种拓扑关系。在计算机处理中常采用链表的数据结构记录几何信息和拓扑信息，即建立顶点表、棱线表、面表和体表。