【机器人】操作与运动控制原理

引言

2025年，机器人技术迎来前所未有的发展机遇。随着人工智能、传感器技术和计算能力的不断进步，现代机器人系统正从传统的程序化执行向真正的智能自主系统演进。本文将全面回顾当前机器人技术的核心领域进展，涵盖感知、规划、控制和学习等方面。

1. 生物学中的操控能力

1.1 动物的操控能力

在众多动物类群中，操控能力与智力之间存在显著相关性。拥有特殊附肢（如灵长类的手、大象的长鼻、章鱼的触腕、鸦科鸟类的喙）的物种通常表现出更高级的认知能力。

尽管这种关系并非普遍存在，但复杂操控能力的形成常与更高的智力共同进化，二者在问题解决、工具使用及环境适应中相互强化。

1.2 最聪明的动物

以下动物被认为具有高度智能：

• 黑猩猩（Chimpanzees）
• 海豚（Dolphin）
• 章鱼（Octopi）
• 大象（Elephant）
• 红猩猩（Orangutans）
• 乌鸦（Crows）

值得注意的是，章鱼的神经元约有 60–70% 分布在外周神经节中，而非集中在大脑，这使得其神经系统结构与其他动物截然不同。

1.3 大脑结构与操控能力

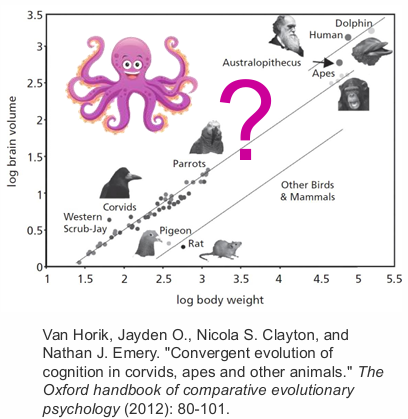
图说明：纵轴为脑容量（log brain volume），横轴为体重对数（log body weight）。图中展示了不同动物在脑容量与体重之间的分布关系：从鸽子、鹦鹉、鸦科鸟类、古人类（Australopithecus）、猿类、人类到海豚。章鱼被标注了一个问号，表示其脑结构与其他动物截然不同，尽管拥有高智能，但不遵循相同的脑-体比例规律。

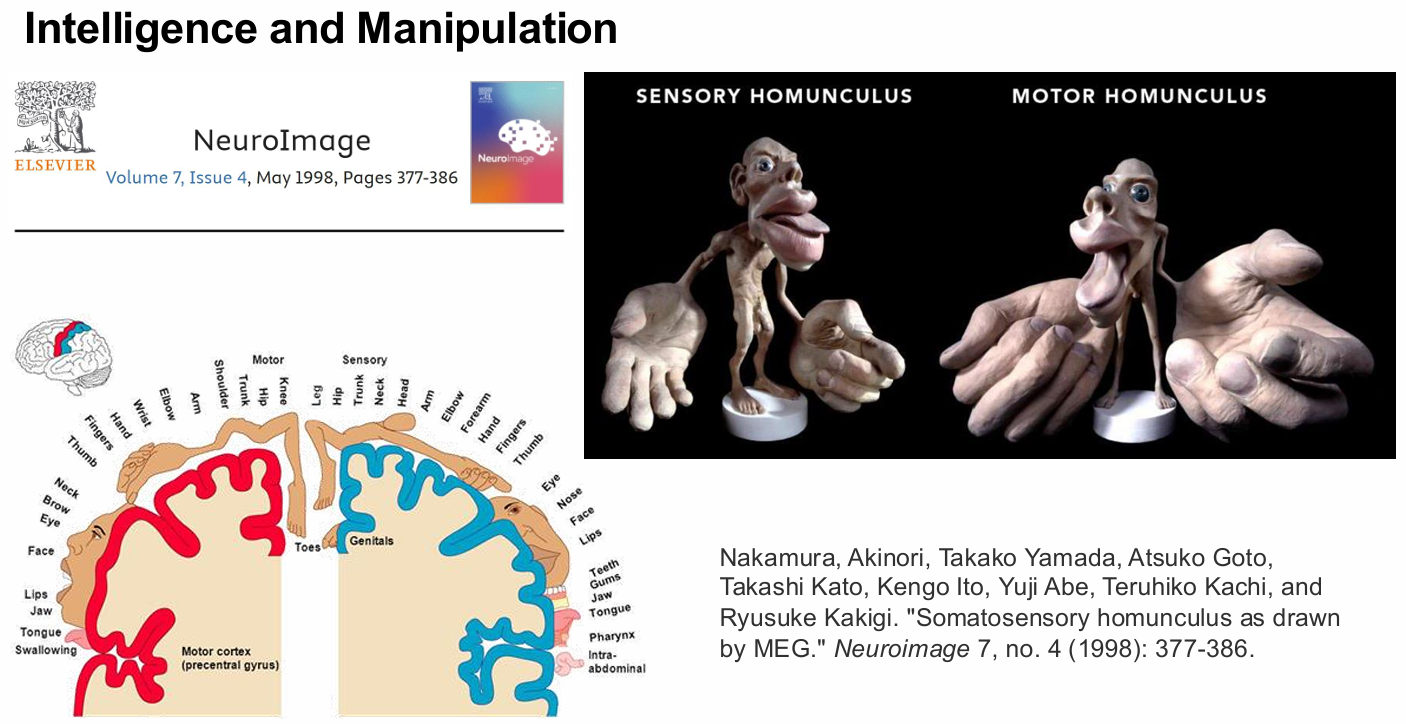
大脑皮层中负责身体不同部位的区域被夸张地拟人化后形成了“脑小人”模型：

• 感觉小人（Sensory Homunculus）：表示身体各部位在躯体感觉皮层中所占比例。
• 运动小人（Motor Homunculus）：表示身体各部位在运动皮层中所占比例。

这些模型突出了手、嘴唇、舌头等部位在感知与操控中的重要性。

2. 刚体运动学基础

2.1 旋转矩阵与姿态表示

旋转矩阵 $ R \in SO(3) $ 表示刚体的姿态方向，是一个 $ 3 \times 3 $ 的正交矩阵，满足：

$$
R^\top R = I, \quad \det® = 1
$$

在三维空间中，旋转矩阵有 3 个自由度，分别对应绕 x、y、z 轴的旋转。

2.2 位置与速度关系

$$
\dot{p} = v
$$

位置向量 $ p \in \mathbb{R}^3 $ 的时间导数是线速度向量 $ v $，表示刚体在惯性坐标系中的平移速度。

2.3 旋转与角速度关系

旋转矩阵随时间的变化由角速度向量 $ \omega \in \mathbb{R}^3 $ 描述：

$$
\dot{R} = R [\omega]_\times
$$

其中 $ [\omega]_\times $ 是由角速度构成的反对称矩阵：

$$
[\omega]_\times =
\begin{bmatrix}
0 & -\omega_z & \omega_y \\
\omega_z & 0 & -\omega_x \\
-\omega_y & \omega_x & 0
\end{bmatrix}
$$

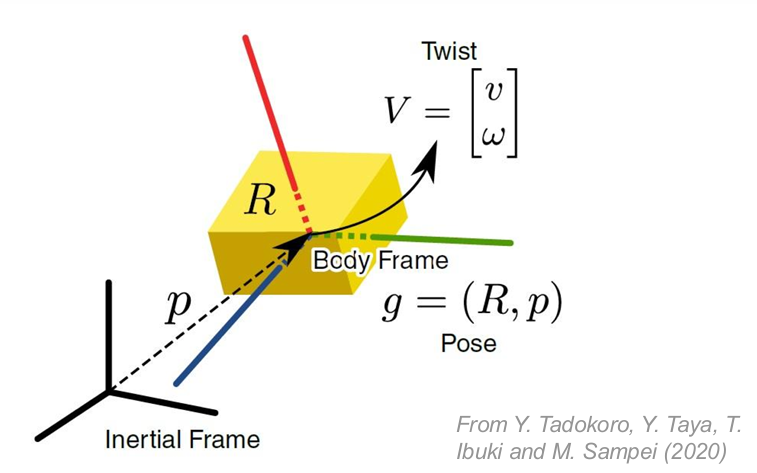
2.4 刚体位姿与速度扭量

刚体在空间中的位姿由下式定义：

$$
g = (R, p) \in SE(3)
$$

其中：

• $ R $：姿态（Orientation）
• $ p $：位置（Position）

线速度 $ v $ 与角速度 $ \omega $ 可组合成扭量向量：

$$
V =
\begin{bmatrix}
v \
\omega
\end{bmatrix}
\in \mathbb{R}^6
$$

扭量 $ V $ 描述了刚体在空间中的线性与旋转运动状态。

直观理解

• 惯性坐标系：固定的空间参考系。
• 刚体坐标系：随刚体移动的参考系。
• 位姿 $ g = (R, p) $：刚体相对于惯性系的位置与姿态。
• 扭量 $ V = [v; \omega] $：刚体此刻的速度状态。

3. 泊松公式

泊松公式（Poisson Equation）如下：

$$
\dot{e}_i = \omega \times e_i
$$

该公式表明，刚体坐标系中每一个固定轴向量 $ e_i $ 的时间导数等于角速度向量 $ \omega $ 与该轴向量的叉积。

3.1 反求公式

通过泊松公式可以反推出角速度向量：

$$
\omega = (\dot{e}_2 \cdot e_3) e_1 + (\dot{e}_3 \cdot e_1) e_2 + (\dot{e}_1 \cdot e_2) e_3
$$

解释：

• $ \dot{e}_i $：坐标轴的变化速率
• $ \omega $：整体角速度
• “·” 表示点积，“×” 表示叉积

这个公式是连接旋转矩阵时间导数与角速度的关键桥梁之一。

4. 机械臂类型

4.1 串联机械臂（Serial Manipulator）

典型代表：UR机械臂、协作机器人等。

• 特点：关节逐级连接，末端自由度由各关节叠加获得。
• 优点：
  • 工作空间大
  • 结构灵活，适合复杂路径规划
• 缺点：
  • 刚度较低
  • 误差累积
  • 动态响应较慢

4.2 并联机械臂（Parallel Manipulator）

典型代表：Delta 机器人、高速分拣机器人。

• 特点：末端由多个支链共同驱动，结构闭环。
• 优点：
  • 刚度高
  • 质量轻，加速度高，适合高速作业
• 缺点：
  • 工作空间较小
  • 运动学分析复杂

4.3 混合型机械臂（Hybrid Manipulator）

典型代表：ABB 工业机器人、装配/搬运机器人。

• 特点：综合串联与并联结构优点。
• 优点：
  • 刚度与灵活性平衡
  • 能在较大空间内保持高负载能力
  • 实现高速、大范围搬运
• 缺点：
  • 结构复杂，成本高
  • 控制系统设计难度大

4.4 类型对比总结

类型	工作空间	刚度	加速度	应用场景
串联型	⭐⭐⭐⭐	⭐⭐	⭐⭐	协作机器人、灵巧操作
并联型	⭐⭐	⭐⭐⭐⭐	⭐⭐⭐⭐	高速分拣、精密装配
混合型	⭐⭐⭐	⭐⭐⭐	⭐⭐⭐	工业搬运、喷涂、焊接

📌 一句话总结：

串联系统“灵活但软”，并联系统“刚且快”，混合系统“折中且强”。

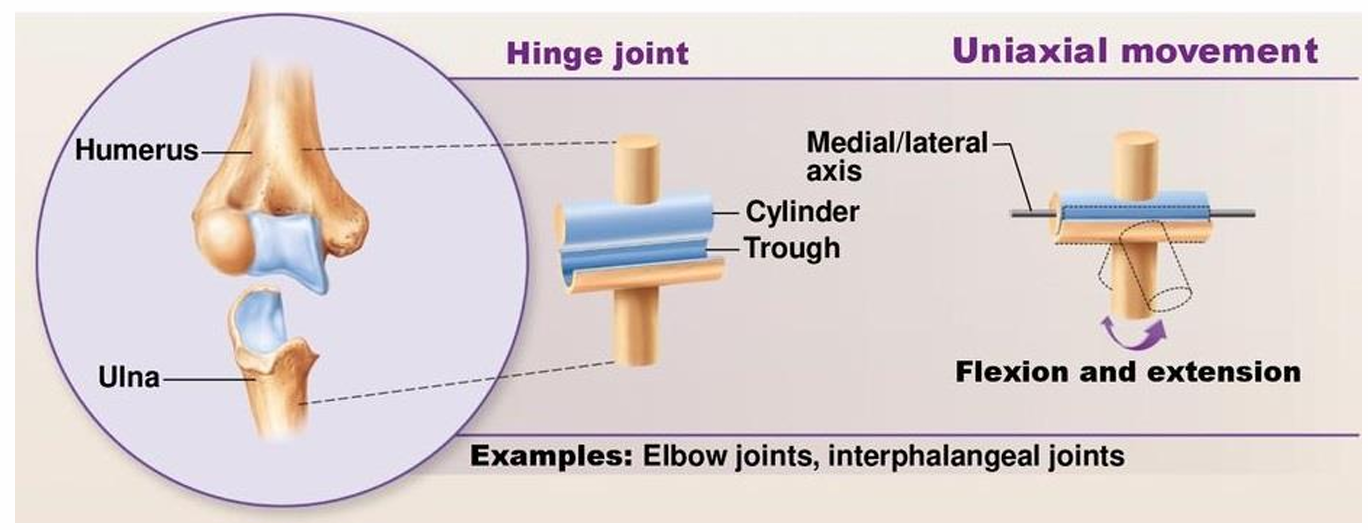
5. 人体手臂与机械臂的类比

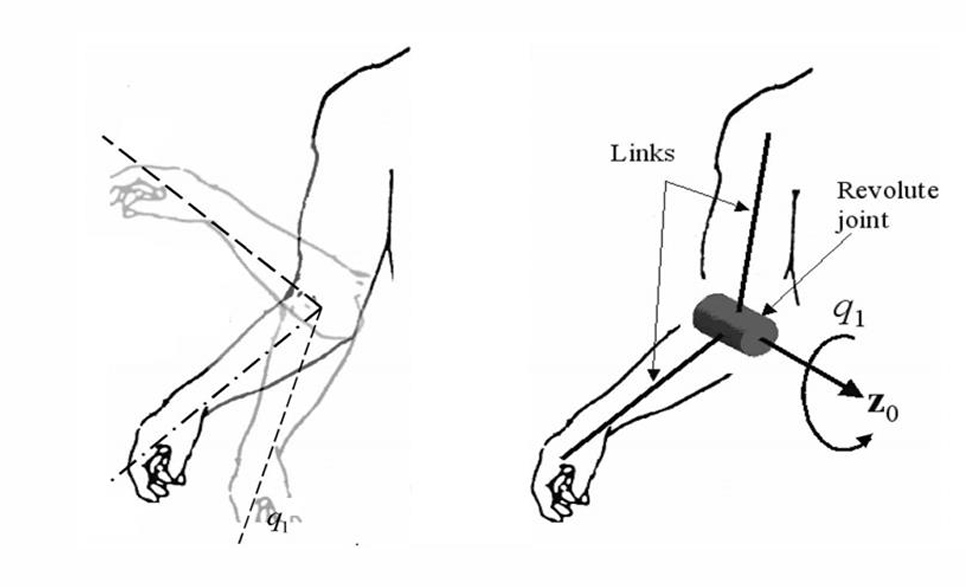
5.1 单自由度旋转关节模型

人体的肘关节可抽象为一个典型的单自由度旋转关节（revolute joint），手臂运动等价于两段连杆绕同一旋转轴运动的机械臂模型。

• 展示手臂在屈伸运动中的姿态变化
• 关节角度记为 $ q_1 $

5.2 模型对应关系

人体部位	机械臂模型元素	含义
肩到肘的上臂	第一根连杆（Link 1）	固定部分
肘到手的前臂	第二根连杆（Link 2）	运动部分
肘关节	旋转关节	角度变化 $ q_1 $
肘关节旋转轴	$ z_0 $	关节旋转方向

5.3 运动学解释

旋转关节的基本运动公式为：

$$
\mathbf{R}(q_1) =
\begin{bmatrix}
\cos q_1 & -\sin q_1 & 0 \
\sin q_1 & \cos q_1 & 0 \
0 & 0 & 1
\end{bmatrix}
$$

• 当角度 $ q_1 $ 改变时，前臂位置随之旋转
• 这是刚体旋转运动的典型形式
• 是 DH 参数法的基础步骤之一

6. 关节坐标与工作空间

6.1 关节空间（Joint Space）

符号：
$$
q_i, \ \theta_i, \ d_i
$$

这些变量描述机械臂各关节的配置状态：

变量	含义	对应类型
$ q_i $	关节变量	通用符号
$ \theta_i $	旋转角度	旋转关节（Revolute）
$ d_i $	线位移	移动关节（Prismatic）

由所有 $ q_i $ 组成的向量 $ \mathbf{q} = [q_1, q_2, …, q_n]^\top $ 定义了关节空间中的姿态。

6.2 工作空间（Workspace）

符号：
$$
p_i(x, y, z), \quad R_i(p_i, p_j, p_k)
$$

这些变量描述机械臂末端在三维空间中的位置与姿态：

变量	含义	对应
$ p_i(x,y,z) $	末端位置向量	位移
$ R_i $	旋转矩阵	姿态

6.3 正运动学关系

$$
f: \text{Joint Space} \rightarrow \text{Workspace}
$$

即：
$$
(p_i, R_i) = f(q_1, q_2, \dots, q_n)
$$

这就是正运动学（Forward Kinematics）——将关节变量转换为末端执行器的位置和姿态。

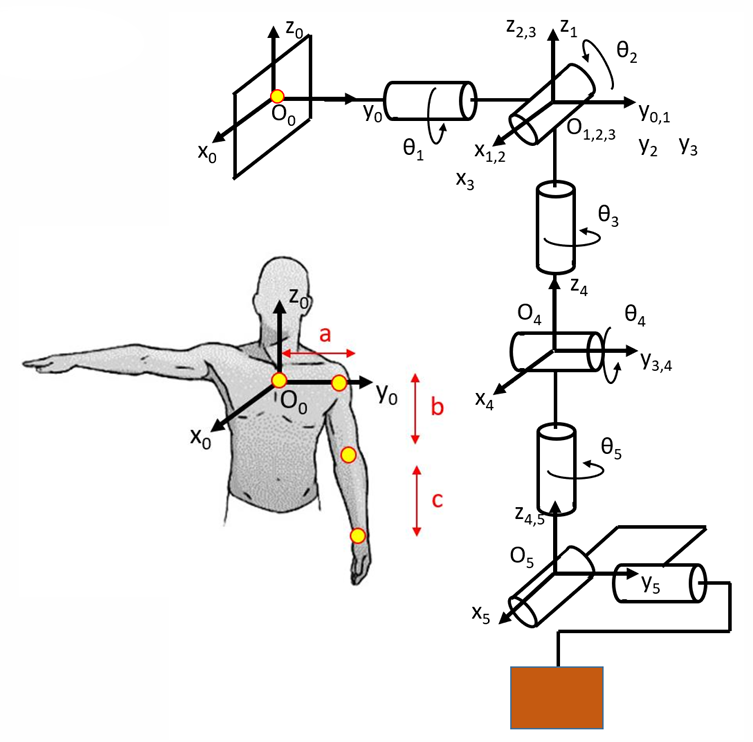
6.4 图示说明

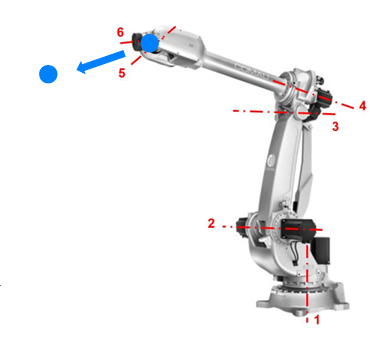
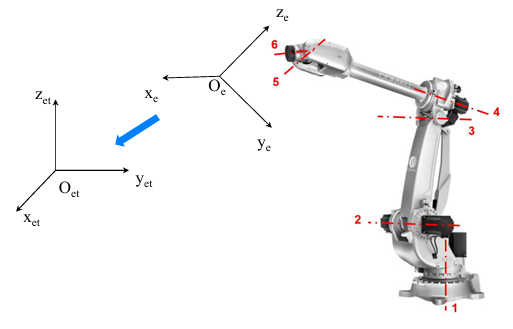
将人体上肢建模为多关节系统（肩、肘、腕），对应机械臂的多自由度结构。

• $ O_0 $：基坐标系
• $ a, b, c $：表示上臂、前臂、手部的连杆长度

展示了一个五关节机械臂的关节坐标系标定过程，各关节角度 $ \theta_1, \theta_2, \dots, \theta_5 $ 对应人体手臂的旋转自由度。

6.5 总结

空间类型	坐标符号	含义	示例
关节空间	$ q_i, \theta_i, d_i $	机械臂关节的旋转/位移	肩关节角度、肘关节角度
工作空间	$ p_i(x,y,z), R_i $	末端执行器的位置与姿态	手部在空间中的位置与方向

📌 一句话总结：

关节空间描述“如何动”（内部角度变化），
工作空间描述“动到哪”（外部位置姿态）。

7. 力闭合（Force Closure）

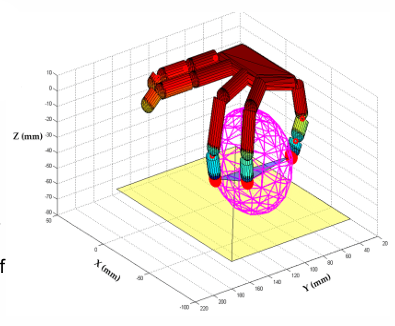
7.1 定义

当机械手（如手指或夹爪）与物体的接触能产生任意方向的力和力矩（wrench），使物体能够抵抗所有外部干扰并保持稳定时，我们称该抓取具有力闭合（Force Closure）。

7.2 特性说明 ✳️

• 抓取可抵抗任意外力与外力矩（external forces and torques）；
• 物体在受到任何方向的扰动时仍不会移动；
• 是否具备力闭合取决于：
  • 接触点的位置（contact locations）；
  • 接触点的摩擦特性（friction properties）。

7.3 直观理解 🧠

力闭合意味着：

“无论外界怎么推、拉、扭，物体都牢牢固定。”

图中展示了一个三指机械手包裹抓取球体的情况，
各接触点通过摩擦与力矩共同形成稳定闭合，使物体完全受控。

7.4 摩擦锥（Friction Cones）

在每个接触点处，接触力的方向受摩擦模型限制，只能存在于摩擦锥内部。
若要实现力闭合抓取（force closure grasp），
所有接触点的摩擦锥所覆盖的力方向组合，
必须能够完全张成六维力矩空间（6D wrench space）：
即既能产生任意方向的力（force），又能产生任意方向的力矩（torque）。

7.5 力闭合 vs. 形闭合（Force vs. Form Closure）

类型	特征	摩擦	是否可移动
形闭合（Form closure）	仅靠几何约束锁定物体（被卡住）	不需要摩擦	不能移动
力闭合（Force closure）	通过摩擦 + 接触力共同作用	需要摩擦	不会移动

📘 总结：
形闭合靠“几何限制”，力闭合靠“摩擦+力平衡”。

7.6 最小接触数（Minimal Contacts）

• 二维 (2D)：只需 2 个带摩擦的接触点 即可实现力闭合。
• 三维 (3D)：至少需要
  • 4 个带摩擦的接触点，或
  • 7 个无摩擦的接触点，
    才能保证对物体施加任意 6 维方向的力与力矩。

7.7 为什么是 4 而不是 3？为什么是 7 而不是 6？

• 在三维空间中，物体具有 6 个自由度（3 平移 + 3 旋转）。
• 要实现力闭合，接触力系统必须能在 6D wrench 空间 内产生任意方向的组合。

当接触点太少（如 3 个）时：

• 虽能固定位置，但无法对抗任意旋转扰动；
• 力矩空间未被完全张成。

4 个带摩擦点：

• 每点摩擦锥提供 3 个独立方向分量（切向 + 法向），
• 足以覆盖 6D wrench 空间。

无摩擦情形：

• 每接触仅能产生法向力（1 维），
• 因此至少要 7 个接触点 才能张满 6 维空间。

7.8 总结 ✅

维度	摩擦	最少接触数	原因
2D	有摩擦	2	能抵抗平面内所有力与转矩
3D	有摩擦	4	能覆盖 6D 力矩空间
3D	无摩擦	7	仅靠法向力也能张满 6D 空间

8. 刚体动力学（Rigid Body Dynamics）

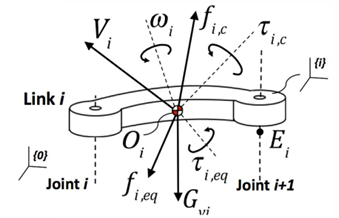
8.1 牛顿–欧拉方程（Newton–Euler Equations）

用于描述刚体（如机械臂连杆）的平动与转动动力学，
由 牛顿定律（平动） 与 欧拉方程（转动） 组合而成。

⚙️ 平动方程（Translation – Newton）

$$
m \ddot{\mathbf{r} }_G = \sum \mathbf{F}_{\text{ext} }
$$

• $ m $：刚体质量
• $ \ddot{\mathbf{r} }_G $：质心加速度
• $ \sum \mathbf{F}_{\text{ext} } $：外力总和

👉 表示：外力 = 质量 × 加速度

🔁 转动方程（Rotation – Euler）

$$
I_G \dot{\omega} + \omega \times (I_G \omega) = \sum \tau_{G,\mathrm{ext} }
$$

• $ \mathbf{I}_G $：质心处惯性张量
• $ \boldsymbol{\omega} $：角速度
• $ \sum \boldsymbol{\tau}_{G,\text{ext} } $：外力矩总和

👉 表示：角动量的变化率 = 外力矩

8.2 图示符号说明

符号	含义
$ G_i $	连杆 $ i $ 的质心
$ O_i $	连杆坐标系原点
$ f_{i,eq}, \ \tau_{i,eq} $	从相邻连杆传递的等效力与力矩
$ V_i, \ \omega_i $	线速度与角速度
$ I_G $	惯性矩阵
$ f_{i,c}, \ \tau_{i,c} $	关节处反作用力与力矩

8.3 物理意义总结

作用	方程	描述
平动	$ m \ddot{\mathbf{r} }_G = \sum \mathbf{F}_{\text{ext} } $	合力决定质心加速度
转动	$ \mathbf{I}_G \dot{\boldsymbol{\omega} } + \boldsymbol{\omega} \times (\mathbf{I}_G \boldsymbol{\omega}) = \sum \boldsymbol{\tau}_{\text{ext} } $	合力矩决定角加速度

📘 结论：
牛顿–欧拉方程是机械臂动力学的核心，用于逐连杆计算力与力矩传播，
并推导机器人动力学方程。

9. 非模型控制方法（Non-model Based Control）

9.1 概念

非模型控制依赖数据与学习，而非精确的物理建模。
特别适用于 软体机器人 或 复杂非线性系统，这些系统难以建立解析模型但可通过数据观测。

9.2 案例：RNN + 运动学混合控制器

论文来源： IEEE RA-L, IROS 2024
研究团队： EPFL Dr. Josie Hughes（博士生 Zixi Chen）

该方法结合 循环神经网络 (RNN/LSTM) 与 运动学控制，
实现对复杂系统的在线控制。

结构组成：

1. 输入： 期望轨迹 (desired trajectory)
2. 核心模块：
   • LSTM 模型： 学习动态与非线性行为
   • 运动学模块： 保证几何约束与可达性
3. 输出： 加权融合后的控制信号（位置 + 驱动），直接作用于机器人系统。

9.3 特点与优势

特性	表现
开环精度高	无需复杂建模即可精确轨迹跟踪
大工作空间	能实现柔顺大范围动作
高顺应性（Compliance）	自然适应外界干扰与接触
在线学习能力	LSTM 动态调整控制策略，提高鲁棒性

📘 总结：
非模型控制将学习算法与运动学结合，
使机器人在复杂环境中实现高精度与高柔顺度控制，
无需完整动力学方程。

10. 模仿学习（Imitation Learning / 行为克隆）

10.1 核心概念

模仿学习通过观察人类示范让机器人学会任务行为，
无需显式建模环境或定义奖励函数。

机器人学习一个策略 $ \pi(a|s) $，
使其在相似状态 $ s $ 下执行与人类相同的动作 $ a $。

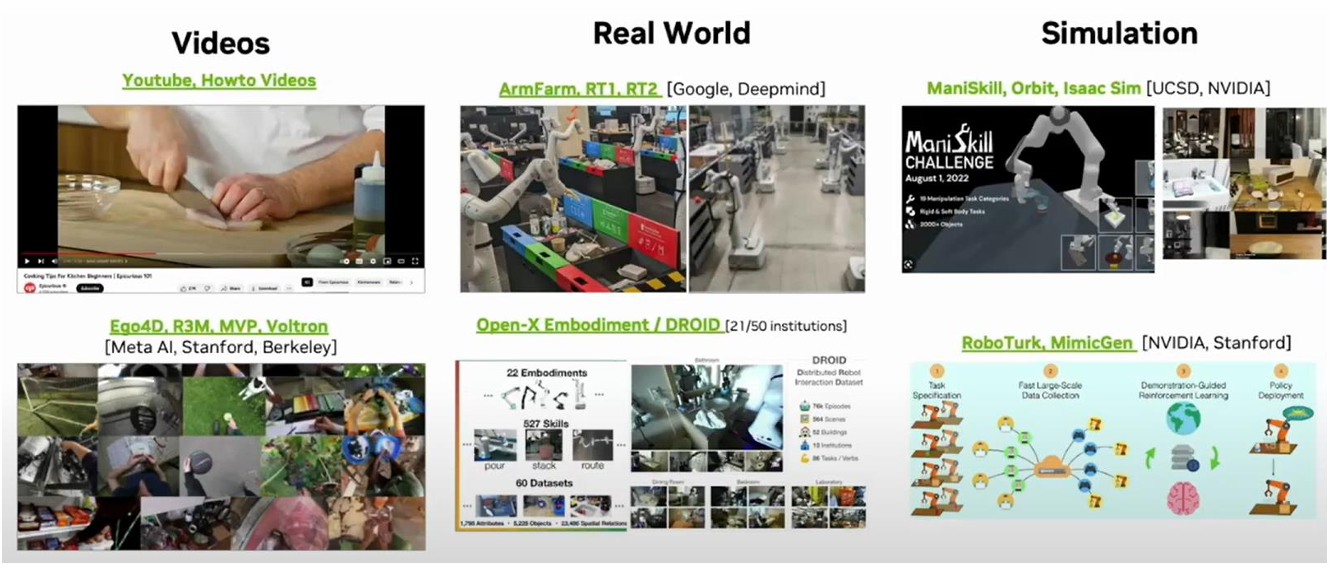
10.2 数据来源 📺

• YouTube / HowTo 视频： 从人类教学视频中提取动作序列；
• Ego4D, R3M, MVP, Voltron（Meta, Stanford, Berkeley）：
  通过第一人称视角数据学习手部操作与视觉语义。

10.3 现实世界应用 🤖

• ArmFarm, RT1, RT2（Google, DeepMind）：
  大规模真实机械臂模仿数据集。
• Open-X Embodiment / DROID：
  全球 20+ 机构合作，涵盖：
  • 22 种机器人形态
  • 500+ 技能
  • 60+ 数据集

10.4 仿真环境 🧩

• ManiSkill, Orbit, Isaac Sim（UCSD, NVIDIA）：
  高保真仿真用于任务学习与评测。
• RoboTurk, MimicGen（Stanford, NVIDIA）：
  基于人类遥操作采集演示数据，
  支持模仿学习 + 强化学习联合训练。

10.5 一句话总结 🧠

模仿学习让机器人“看人做事”后，学会“自己动手”。
数据可来自视频、真实操作或仿真演示，
是通向通用机器人智能的重要路径之一。

来源： Dr. Dieter Fox, NVIDIA

11. 机器人微分运动学与雅可比矩阵（Differential Kinematics and Jacobian）

11.1 微分运动学基本关系

在机器人学中，微分运动学（Differential Kinematics）描述了关节速度与末端执行器线速度/角速度之间的映射关系。

数学表达为：

$$
\mathbf{v} = \mathbf{J(q)} \cdot \dot{\mathbf{q} }
$$

其中：

符号	含义
$\mathbf{q} \in \mathbb{R}^n$	关节变量（Joint Angles / Displacements）
$\dot{\mathbf{q} } \in \mathbb{R}^n$	关节速度（Joint Velocities）
$\mathbf{v} \in \mathbb{R}^6$	末端速度（Twist: [Linear; Angular]）
$\mathbf{J(q)} \in \mathbb{R}^{6 \times n}$	雅可比矩阵（Jacobian Matrix）

11.2 雅可比矩阵的物理意义

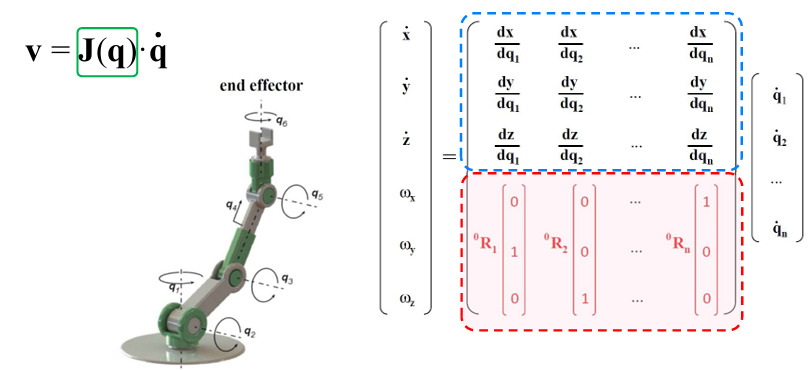
雅可比矩阵的每一列，表示当单个关节以单位角速度运动时，末端线速度和角速度的贡献。

Jacobian 是“关节空间 → 工作空间”速度映射的核心桥梁。

• 上半部分（蓝框）表示线速度对关节速度的映射；
• 下半部分（红框）表示角速度对关节速度的映射。

11.3 旋转部分的雅可比矩阵（Rotational Part of Jacobian）

旋转部分由各关节的角速度累积贡献组成：

$$
{}^{0}\omega_{6/wrt,0} =
{}^{0}\mathbf{R}_1 \hat{\mathbf{z} }_1 \dot{q}_1 +
{}^{0}\mathbf{R}_2 \hat{\mathbf{z} }_2 \dot{q}_2 +
{}^{0}\mathbf{R}_3 \hat{\mathbf{z} }_3 \dot{q}_3 +
{}^{0}\mathbf{R}_4 \hat{\mathbf{z} }_4 \dot{q}_4 +
{}^{0}\mathbf{R}_5 \hat{\mathbf{z} }_5 \dot{q}_5 +
{}^{0}\mathbf{R}_6 \hat{\mathbf{z} }_6 \dot{q}_6
$$

其中：

• $\hat{\mathbf{z} }_i$：第 $i$ 个关节的旋转轴方向
• ${}^{0}\mathbf{R}_i$：从第 $i$ 坐标系到基坐标系的旋转矩阵
• $\dot{q}_i$：关节角速度

11.4 雅可比矩阵的结构分块

完整的雅可比矩阵可分为两部分：

$$
\mathbf{J} =
\begin{bmatrix}
\mathbf{J}_v \\
\mathbf{J}_\omega
\end{bmatrix}
$$

部分	含义	对应方程
$\mathbf{J}_v$	线速度部分	$\dot{\mathbf{p} } = \mathbf{J}_v \dot{\mathbf{q} }$
$\mathbf{J}_\omega$	角速度部分	$\boldsymbol{\omega} = \mathbf{J}_\omega \dot{\mathbf{q} }$

11.5 雅可比矩阵的应用

应用场景	说明
运动学控制	根据目标末端速度求解所需关节速度： $\dot{\mathbf{q} } = \mathbf{J}^{-1}\mathbf{v}$
力控制	雅可比矩阵可将力/力矩从末端映射到关节空间： $\boldsymbol{\tau} = \mathbf{J}^T \mathbf{F}$
奇异性分析	当 $\det(\mathbf{J}\mathbf{J}^T) = 0$ 时，系统失去某些方向的运动能力
冗余度控制	若 $n > 6$，使用伪逆 $\mathbf{J}^+$ 实现最小范数或二级优化控制

11.6 直观理解 🧩

• 雅可比矩阵像一个“齿轮系”：
  每个关节转动一点，末端的线速度和角速度都被“放大或缩小”地传递。
• 它连接了：
  • 运动学（位置）
  • 动力学（力）
  • 控制（反馈与规划）

📘 一句话总结：

雅可比矩阵是机器人控制的“核心导数”，
它连接了几何、运动与力学的三个世界。

12. 雅可比逆与运动控制（Inverse Jacobian and Motion Control）

12.1 从目标速度到关节速度的反向映射

在前一节中，我们看到雅可比矩阵用于描述关节速度 → 末端速度的正向映射：

$$
\mathbf{v} = \mathbf{J(q)} , \dot{\mathbf{q} }
$$

若已知末端执行器的速度 $\mathbf{v}$，我们希望反推出各关节应当以何种速度运动以实现该目标，则可使用雅可比逆（Inverse Jacobian）：

$$
\dot{\mathbf{q} } = \mathbf{J}^{-1}(\mathbf{q}) , \mathbf{v}
$$

即：通过逆雅可比矩阵，将末端速度映射回关节速度空间。

12.2 位置控制（Position Control）

在执行从初始位置到目标位置的运动时，我们通常已知：

• 方向（由起点和终点决定）与距离（路径长度）；
• 期望执行时间（Desired execution time）；
• 通过时间微分可得线速度 $\mathbf{v}$。

因此，可以逐步迭代求解：

$$
\dot{\mathbf{q} } = \mathbf{J}^{-1}(\mathbf{q}) , \mathbf{v}
$$

通过积分 $\dot{\mathbf{q} }$，即可更新每个时刻的关节角度，实现末端沿目标方向平滑运动。

12.3 姿态控制（Orientation Control）

对于姿态控制，我们不仅关心位置变化，还要使末端的**方向矩阵（Orientation Matrix）**从初始朝向旋转到目标朝向。

已知：

• 初始旋转矩阵 $R_i$
• 目标旋转矩阵 $R_f$
• 期望执行时间 $t_f$

则控制目标是求解旋转轴与角速度向量 $\boldsymbol{\omega}$，即：

“以哪个方向旋转、以多快的速度旋转？”

由雅可比逆关系：

$$
\dot{\mathbf{q} } = \mathbf{J}^{-1}(\mathbf{q}) , \mathbf{v}
$$

其中 $\mathbf{v}$ 的角速度分量由 $\boldsymbol{\omega}$ 提供。

12.4 从旋转矩阵计算旋转向量

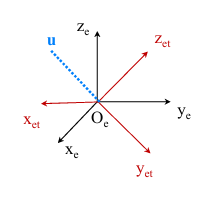
设旋转矩阵：

$$
R =
\begin{bmatrix}
a & b & c \\
d & e & f \\
g & h & i
\end{bmatrix}
$$

旋转向量 $\mathbf{u}$ 定义为：

$$
\mathbf{u} =
\begin{bmatrix}
h - f \\
c - g \\
d - b
\end{bmatrix},
\quad |\mathbf{u}| = 2 \sin \theta
$$

其中：

• $\mathbf{u}$ 的方向为旋转轴；
• $|\mathbf{u}|$ 的大小与旋转角度 $\theta$ 成正比。

12.5 雅可比伪逆（Jacobian Pseudoinverse）

当机械臂冗余自由度 $n > 6$ 或存在奇异点时，$\mathbf{J}$ 不可逆。
此时可采用 广义逆（Moore–Penrose Pseudoinverse）：

$$
\mathbf{J}^{+} = \mathbf{J}^T (\mathbf{J}\mathbf{J}^T)^{-1}
$$

并使用：

$$
\dot{\mathbf{q} } = \mathbf{J}^{+}(\mathbf{q}) , \mathbf{v}
$$

该解满足最小范数条件，保证末端速度最优匹配。

13. 雅可比矩阵的维度与形态分类（Jacobian Dimension and Shape Summary）

雅可比矩阵 $\mathbf{J(q)}$ 将关节速度 $\dot{\mathbf{q} }$ 与末端速度 $\mathbf{v}$ 联系起来：

$$
\mathbf{v} = \mathbf{J(q)} , \dot{\mathbf{q} }
$$

其矩阵维度为：

$$
\mathbf{v} \in \mathbb{R}^{6 \times 1}, \quad
\mathbf{J(q)} \in \mathbb{R}^{6 \times n}, \quad
\dot{\mathbf{q} } \in \mathbb{R}^{n \times 1}
$$

因此，系统的解空间取决于关节数 $n$ 与任务空间维度（6，自由移动与旋转）的关系：

13.1 三种情形（Three Cases）

情形	说明	解的数量
$n < 6$	欠驱动（Under-actuated）系统，通常无精确解	无解（No exact solution）
$n = 6$	完全驱动（Fully-actuated）系统，雅可比矩阵为方阵	唯一解（One exact solution）
$n > 6$	冗余驱动（Over-actuated）系统，末端可由多种关节组合实现	无穷多解（Infinite solutions）

13.2 雅可比矩阵的形态分类（Jacobian Shape Summary）

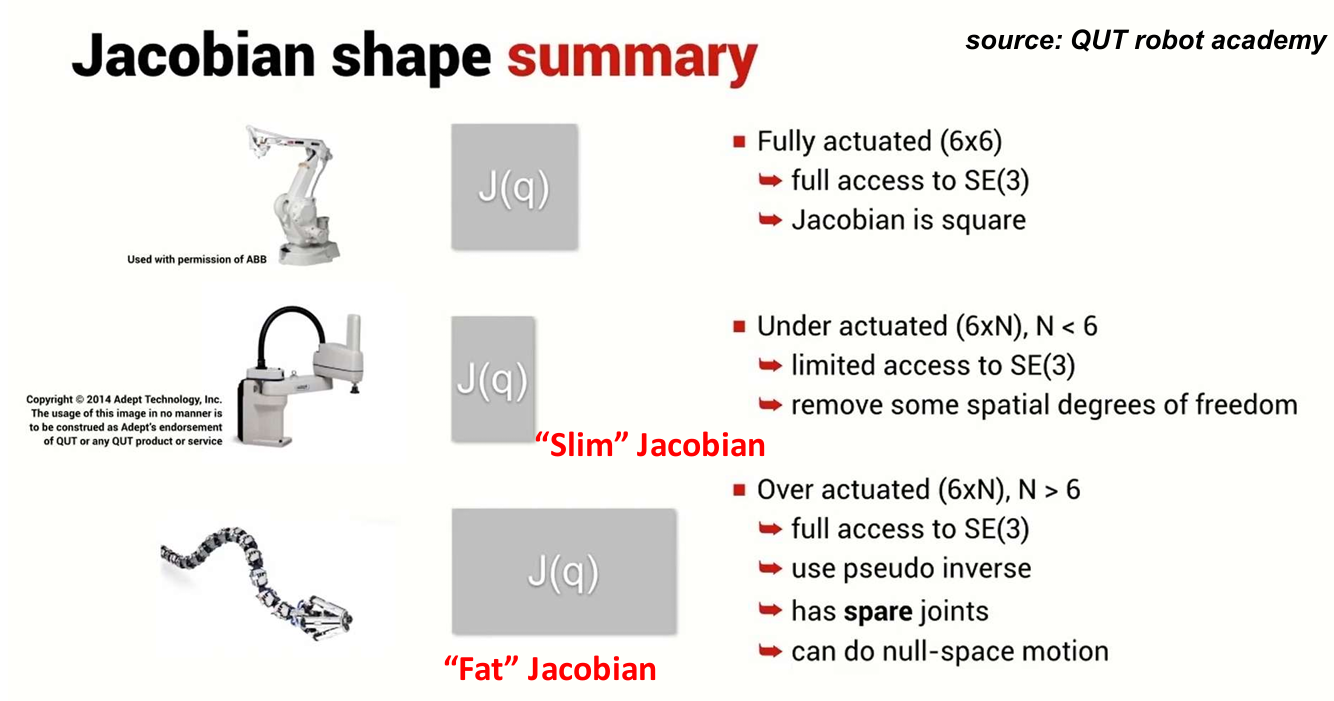
不同的机械臂结构会导致雅可比矩阵 $\mathbf{J(q)}$ 的形态（shape）不同，
反映出系统的**可控性（actuation）与运动自由度（DoF）**特征。
根据关节数 $N$ 与任务空间维度（通常为 6，自由移动与旋转）之间的关系，
我们可以将雅可比矩阵分为三类：Square / Slim / Fat Jacobian。

① 方形雅可比矩阵（Square Jacobian）

条件：
$$ N = 6 $$
$$ \mathbf{J(q)} \in \mathbb{R}^{6 \times 6} $$

特征：

• 完全驱动（Fully actuated）；
• 对 $SE(3)$（三维刚体运动群）具有完整控制；
• 雅可比矩阵可逆；
• 典型代表：六轴工业机械臂（如 ABB、KUKA、UR）。

优点：

• 可以直接计算逆矩阵 $\mathbf{J}^{-1}$；
• 运动学与动力学求解简洁。

② 瘦雅可比矩阵（Slim Jacobian）

条件：
$$ N < 6 $$
$$ \mathbf{J(q)} \in \mathbb{R}^{6 \times N}, \quad N < 6 $$

特征：

• 欠驱动系统（Under-actuated）；
• 对 $SE(3)$ 的访问受限；
• 无法独立控制全部 6 个空间自由度；
• 通常用于平面机械臂（如 SCARA 机械臂）。

结果：

• 系统丢失部分姿态或方向控制；
• 某些任务空间方向上无法施加速度或力。

③ 胖雅可比矩阵（Fat Jacobian）

条件：
$$ N > 6 $$
$$ \mathbf{J(q)} \in \mathbb{R}^{6 \times N}, \quad N > 6 $$

特征：

• 冗余驱动系统（Over-actuated / Redundant manipulator）；
• 对 $SE(3)$ 拥有完全访问能力；
• 可使用伪逆 $\mathbf{J}^{+}$ 来计算最优关节速度；
• 存在冗余关节（spare joints）；
• 可进行零空间运动（Null-space motion）。

应用：

• 避障控制（Obstacle avoidance）；
• 能量最小化（Energy optimization）；
• 次级任务规划（Secondary task planning）；
• 柔性或蛇形机器人、连续体机械臂等。

📊 三种雅可比矩阵形态对比

类型	条件	特征	典型系统	逆矩阵类型
方形（Square）	$N = 6$	完全驱动	六轴机械臂	$\mathbf{J}^{-1}$
瘦型（Slim）	$N < 6$	欠驱动	SCARA、2D机械臂	无逆（欠约束）
胖型（Fat）	$N > 6$	冗余驱动	柔性、蛇形臂	$\mathbf{J}^{+}$（伪逆）

13.3 伪逆（Pseudoinverse）与最优解

当雅可比矩阵 $\mathbf{J(q)}$ 不可逆（例如 $N \neq 6$ 或奇异状态）时，
我们使用 Moore–Penrose 伪逆（Pseudoinverse） 来求得最优近似解：

(1) 欠约束系统（Under-constrained, $N < 6$）

$$
\mathbf{J}^{+} = \mathbf{J}^{T} , (\mathbf{J}\mathbf{J}^{T})^{-1}
$$

该形式最小化关节速度范数：

$$
\min | \dot{\mathbf{q} } |
$$

即找到使末端运动尽量匹配、同时关节速度最小的解。

(2) 过约束系统（Over-constrained, $N > 6$）

$$
\mathbf{J}^{+} = (\mathbf{J}^{T}\mathbf{J})^{-1} , \mathbf{J}^{T}
$$

该形式最小化末端误差：

$$
\min | \mathbf{J}\dot{\mathbf{q} } - \dot{\mathbf{x} } |
$$

保证末端运动的最小均方误差（Least Squares Solution）。

📘 总结：

系统类型	伪逆形式	优化目标
欠驱动 ($N < 6$)	$\mathbf{J}^{+} = \mathbf{J}^{T}(\mathbf{J}\mathbf{J}^{T})^{-1}$	最小化 $|\dot{\mathbf{q} }|$
冗余驱动 ($N > 6$)	$\mathbf{J}^{+} = (\mathbf{J}^{T}\mathbf{J})^{-1}\mathbf{J}^{T}$	最小化 $|\mathbf{J}\dot{\mathbf{q} } - \dot{\mathbf{x} }|$

📖 一句话总结：

当雅可比矩阵不可逆时，伪逆提供了最“合理”的近似解，
欠约束系统追求最小关节运动，冗余系统追求最小误差。

14. 状态空间表示（State Space Representation）

14.1 定义与基本思想

状态空间模型（State-Space Model）是一种以一阶微分方程组形式描述物理系统行为的数学模型。
它将系统的动态特性用状态变量（state variables）、**输入（inputs）和输出（outputs）**表示。

系统状态空间方程一般写为：

$$
\dot{x}(t) = A x(t) + B u(t)
$$
$$
y(t) = C x(t) + D u(t)
$$

其中：

符号	含义
$x(t)$	状态向量（State Vector）
$\dot{x}(t)$	状态向量的一阶导数（随时间变化率）
$u(t)$	输入或控制向量（Input / Control Vector）
$y(t)$	输出向量（Output Vector）
$A$	系统矩阵（System Matrix）
$B$	输入矩阵（Input Matrix）
$C$	输出矩阵（Output Matrix）
$D$	直接传输矩阵（Feedforward Matrix）

📘 直观理解：

• 状态变量（State variables）：表示系统的记忆，例如位置、速度、电流等。
• 输入（Inputs）：表示外部激励，如力、转矩、电压信号。
• 输出（Outputs）：表示可测量的系统响应，如位移、速度、角度等。

14.2 单输入单输出系统（SISO, Single-Input Single-Output）

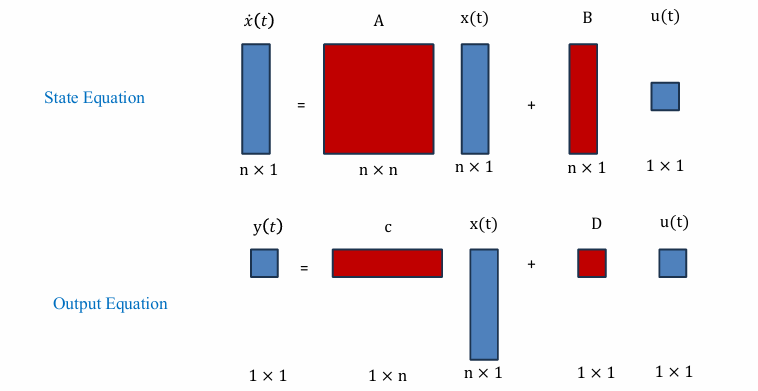
在 SISO 系统中，系统只有一个输入和一个输出：

$$
\dot{x}(t) = A x(t) + B u(t)
$$
$$
y(t) = C x(t) + D u(t)
$$

矩阵维度如下：

矩阵/变量	维度	说明
$x(t)$	$n \times 1$	状态向量
$\dot{x}(t)$	$n \times 1$	状态导数
$u(t)$	$1 \times 1$	单输入
$y(t)$	$1 \times 1$	单输出
$A$	$n \times n$	系统矩阵
$B$	$n \times 1$	输入矩阵
$C$	$1 \times n$	输出矩阵
$D$	$1 \times 1$	直接传输矩阵

📖 理解要点：

• 状态方程决定系统的动态特性；
• 输出方程描述状态与输出的映射；
• SISO 模型在机械臂单关节、单电机或单回路控制中广泛应用。

14.3 多输入多输出系统（MIMO, Multi-Input Multi-Output）

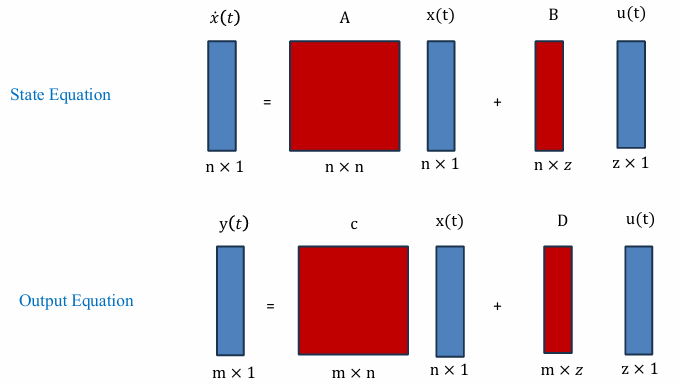
当系统具有多个输入与多个输出时，模型扩展为 MIMO 形式：

$$
\dot{x}(t) = A x(t) + B u(t)
$$
$$
y(t) = C x(t) + D u(t)
$$

矩阵维度如下：

矩阵/变量	维度	说明
$x(t)$	$n \times 1$	状态向量
$\dot{x}(t)$	$n \times 1$	状态导数
$u(t)$	$z \times 1$	$z$ 个输入（多控制信号）
$y(t)$	$m \times 1$	$m$ 个输出（多观测量）
$A$	$n \times n$	系统矩阵
$B$	$n \times z$	输入矩阵
$C$	$m \times n$	输出矩阵
$D$	$m \times z$	直接传输矩阵

14.4 状态空间模型的优势

✅ 统一性：
适用于线性与非线性系统、连续与离散系统。

✅ 可扩展性：
易于扩展到高维、耦合系统。

✅ 分析便利：
便于求解稳定性、可控性（Controllability）、可观性（Observability）。

✅ 现代控制基础：
是 PID 控制、最优控制、LQR、状态反馈等方法的核心数学基础。

📘 一句话总结：

状态空间模型是将系统动态从“输入-输出关系”推广到“内部状态演化”的现代控制理论核心形式，
为复杂机械臂与多自由度系统的建模与控制提供了统一框架。

15. 非线性系统与线性化控制（Nonlinear Systems and Linearization Control）

15.1 非线性系统（Nonlinear Systems）

在现实世界中，大多数机械、电气、生物及机器人系统都是非线性（nonlinear）的。
这意味着它们的动态关系无法完全用线性方程描述。

示例：

• 单摆系统：
  $$
  m l^2 \ddot{\theta} + b \dot{\theta} + m g l \sin(\theta) = T
  $$
• 机械臂动力学（包含三角项和耦合项）；
• 飞行器在湍流作用下的非线性运动。

15.2 为什么非线性是问题？（Why is this a Problem?）

• 非线性方程难以分析（稳定性 controllability、可控性 stability、可观性 observability 等）；
• 许多标准工具（如传递函数 transfer functions、频率响应 frequency response、根轨迹法 root locus）仅适用于线性系统。

15.3 解决方案：线性化（Linearization）

核心思想：

在某个工作点或平衡点附近，用线性系统近似原非线性系统。

线性化后的模型可分为：

• 线性时变系统（LTV, Linear Time-Varying）
• 线性时不变系统（LTI, Linear Time-Invariant）

优点：

• 便于分析与控制；
• 可使用经典线性控制工具（如 PID、LQR、Observer）。

15.4 线性化状态空间模型（Linearized State-Space Model）

对于一个非线性系统：

$$
\dot{x}(t) = f(x(t), u(t)), \quad y(t) = g(x(t), u(t))
$$

我们希望在某个工作点 $(x^{sol}, u^{sol})$ 附近用线性系统来近似它的动态。
这种近似允许我们在小扰动范围内分析系统的稳定性与控制特性。

🧩 最终线性化系统（Final Linearized System）

$$
\delta \dot{x}(t) = A(t),\delta x(t) + B(t),\delta u(t)
$$
$$
\delta y(t) = C(t),\delta x(t) + D(t),\delta u(t)
$$

其中：

• $\delta x(t)$ 表示状态变量相对于工作点的微小偏差；
• $\delta u(t)$ 表示输入的微小变化；
• $\delta y(t)$ 表示输出响应的变化。

📐 雅可比矩阵定义（Jacobian Matrices）

$$
A(t) = \frac{\partial f}{\partial x}(x^{sol}, u^{sol}), \quad
B(t) = \frac{\partial f}{\partial u}(x^{sol}, u^{sol})
$$

$$
C(t) = \frac{\partial g}{\partial x}(x^{sol}, u^{sol}), \quad
D(t) = \frac{\partial g}{\partial u}(x^{sol}, u^{sol})
$$

🤖 与机器人系统的关系（Conceptual Link to Robots）

矩阵	含义	对应物理解释
$A(t)$	状态对自身的影响	关节角、角速度等状态如何相互作用
$B(t)$	输入对状态的影响	控制输入（力矩、推力）如何驱动系统
$C(t)$	状态对输出的影响	内部状态如何通过传感器体现
$D(t)$	输入对输出的直接影响	一般在机械系统中近似为零

💡 工程意义（Practical Meaning）

在机器人学中，这种线性化状态空间模型的意义在于：

• 它让我们能够设计线性控制器（如 LQR、PID、Observer），
  即使系统本质上是非线性的；
• 该模型在局部范围内有效，能使机器人在小扰动下保持预期轨迹；
• 这是分析机器人稳定性与轨迹跟踪误差的核心工具。

📘 总结：

线性化状态空间模型通过在工作点附近的局部线性近似，
将复杂的非线性动力学系统转化为可控、可分析的形式，
从而奠定了现代机器人控制与状态估计的基础。

15.5 平衡点线性化（Linearization about an Equilibrium Point）

在线性系统理论中，我们经常需要将一个非线性系统
在其平衡点（Equilibrium Point）附近进行线性化，以得到一个等效的线性时不变系统（LTI System）。

⚙️ 非线性系统定义

考虑如下非线性状态方程：

$$
\dot{x}(t) = f(x(t), u(t)), \quad y(t) = g(x(t), u(t))
$$

其中：

• $x(t) \in \mathbb{R}^n$ —— 系统状态向量（如位置、速度、角度等）；
• $u(t) \in \mathbb{R}^k$ —— 控制输入（如力矩、电压等）；
• $y(t) \in \mathbb{R}^m$ —— 输出（传感器测量量或系统响应）。

⚖️ 平衡点（Equilibrium Point）

若存在一对 $(x^{eq}, u^{eq})$ 满足：

$$
f(x^{eq}, u^{eq}) = 0
$$

则称该点为系统的平衡点。
此时系统满足：

$$
u(t) = u^{eq}, \quad x(t) = x^{eq}, \quad y(t) = y^{eq} = g(x^{eq}, u^{eq})
$$

这意味着在平衡点处，系统保持静止或匀速运动，状态不再随时间变化。

🔁 平衡点附近线性化（Linearizing around $(x^{eq}, u^{eq})$）

在平衡点附近进行泰勒展开，并忽略高阶项，可得线性近似系统：

$$
\delta \dot{x}(t) = A \delta x(t) + B \delta u(t)
$$
$$
\delta y(t) = C \delta x(t) + D \delta u(t)
$$

其中：

$$
A = \frac{\partial f}{\partial x}(x^{eq}, u^{eq}), \quad
B = \frac{\partial f}{\partial u}(x^{eq}, u^{eq})
$$

$$
C = \frac{\partial g}{\partial x}(x^{eq}, u^{eq}), \quad
D = \frac{\partial g}{\partial u}(x^{eq}, u^{eq})
$$

🧩 系统含义说明

矩阵	含义
$A$	状态变化对自身动态的线性影响（系统固有动力学）
$B$	控制输入对系统状态的影响（外部控制作用）
$C$	状态变化对输出的影响（测量关系）
$D$	输入对输出的直接耦合（机械系统中通常为 0）

💡 工程意义（In Robotics Context）

在机器人控制中，平衡点线性化是建立**线性时不变模型（LTI）**的基础步骤。
例如：

• 在线性化平衡点（如机械臂的静止姿态）附近设计控制器；
• 分析系统在局部扰动下的稳定性（Stability）；
• 构造局部线性模型以实现 LQR、PID、Observer 等控制策略。

📘 总结：

平衡点线性化将复杂的非线性动力学系统转化为局部线性形式，
便于应用经典线性控制理论，实现对系统局部稳定性的分析与控制。

15.6 反馈线性化（Feedback Linearization）

反馈线性化（Feedback Linearization）是一种强大的非线性控制技术，
通过设计非线性反馈控制律，将原始非线性系统转化为等效线性系统，
从而能够应用线性控制理论进行分析与设计。

🧩 定义（Definition）

反馈线性化（Feedback Linearization） 是一种利用非线性反馈控制输入
来抵消系统内部非线性项，使其在输入输出关系上表现为线性系统的控制方法。

数学上，它通过引入输入变换：

$$
u = \alpha(x) + \beta(x)v
$$

其中：

• $\alpha(x)$ —— 非线性补偿项，用于抵消系统的固有非线性；
• $\beta(x)$ —— 输入增益项，用于调整输入信号的作用比例；
• $v$ —— 新的控制输入，用于设计线性控制律。

将系统

$$
\dot{x} = f(x) + g(x)u, \quad y = h(x)
$$

其中：

• $x \in \mathbb{R}^n$ —— 系统状态；
• $u \in \mathbb{R}$ 或 $\mathbb{R}^m$ —— 控制输入；
• $\dot{x}$ —— 状态的时间导数。
• $f(x)$：系统的自然动态项（或漂移项），反映系统在无输入时的自然演化；
• $g(x)$：系统的控制输入通道，决定输入 $u$ 如何影响状态；
• $h(x)$：输出函数，定义可测的系统输出。

变换为线性系统形式：

$$
\dot{x} = A x + B v
$$

其中：

• $A$ 和 $B$ 是常数或局部线性矩阵；
• $v$ 是新的“等效线性输入”；
• 系统在该形式下可以直接应用线性控制工具。

此时，控制输入 $v$ 可以通过常规线性控制器（如 LQR、PID）设计得到。

附：

控制方法	核心思想	优点	缺点	典型应用
PID	基于误差的比例-积分-微分反馈	简单可靠，易实现	难以最优，需调参	工业过程控制、舵机控制
LQR	最小化状态与能量代价	数学上最优控制	需系统模型，线性假设	飞行器姿态、机器人控制

📘 推导过程（Step-by-step Derivation）

将 $u = \alpha(x) + \beta(x)v$ 代入原方程：

$$
\dot{x} = f(x) + g(x)[\alpha(x) + \beta(x)v]
$$

展开：

$$
\dot{x} = [f(x) + g(x)\alpha(x)] + g(x)\beta(x)v
$$

我们希望这个系统能写成线性形式：

$$
\dot{x} = A x + B v
$$

于是只需选择合适的 $\alpha(x)$ 和 $\beta(x)$，使得：

• 第一项 $[f(x) + g(x)\alpha(x)]$ 成为线性函数 $A x$；
• 第二项 $g(x)\beta(x)$ 等价于常数矩阵 $B$。

这就意味着通过 $\alpha(x)$ 的选择，我们“抵消”掉系统中复杂的非线性项，
而通过 $\beta(x)$ 的选择，我们“线性化”输入通道。

💡 为什么需要反馈线性化（Why is it Necessary?）

• 大多数真实系统（如单摆、机械臂、飞行器）本质上都是非线性系统；
• 非线性方程难以进行稳定性分析与控制设计；
• 通过反馈线性化：
  • 使用反馈抵消系统中的非线性项；
  • 系统行为表现为线性时不变（LTI）形式；
  • 可以直接使用经典的线性控制工具。

⚙️ 优势（Key Advantages）

特性	优点
分析方便	系统线性化后便于稳定性与性能分析
控制设计	可使用线性控制器（如 LQR、Observer、Pole Placement）
实际应用	常用于机械臂控制、飞行器姿态控制、移动机器人动态补偿等

📘 示例一：机械臂动力学中的反馈线性化

考虑一个机械臂的动力学模型：

$$
M(q)\ddot{q} + B(q, \dot{q})\dot{q} + G(q) = F
$$

其中：

• $q \in \mathbb{R}^k$ 为关节角向量；
• $F \in \mathbb{R}^k$ 为关节力矩；
• $M(q)$ 是质量惯量矩阵；
• $B(q, \dot{q})$ 表示科氏力与离心力；
• $G(q)$ 是重力项。

🧠 步骤 1：定义新的输入

设控制输入为：

$$
F = u = u_{nl}(q, \dot{q}) + M(q)v
$$

其中非线性补偿项定义为：

$$
u_{nl}(q, \dot{q}) = B(q, \dot{q})\dot{q} + G(q)
$$

⚙️ 步骤 2：代入系统方程

将其代入原动力学方程：

$$
M(q)\ddot{q} + B(q, \dot{q})\dot{q} + G(q) = F
$$

得到：

$$
\ddot{q} = v
$$

这意味着系统的复杂非线性动态被消除，变为简单的双积分系统（Double Integrator）。

🧾 步骤 3：状态空间形式

定义状态向量：

$$
x = \begin{bmatrix} q \ \dot{q} \end{bmatrix} \in \mathbb{R}^{2k}
$$

则系统可以写为：

$$
\dot{x} =
\begin{bmatrix}
0 & I \
0 & 0
\end{bmatrix}
x +
\begin{bmatrix}
0 \
1
\end{bmatrix}
v
$$

📘 示例二：严格反馈形式（Strict Feedback Form）

考虑非线性系统：

$$
\dot{x}_1 = f_1(x_1) + x_2, \quad
\dot{x}_2 = f_2(x_1, x_2) + u
$$

步骤 1：引入新变量

定义新的状态变量：

$$
z_2 := f_1(x_1) + x_2
$$

则有：

$$
\dot{x}_1 = z_2
$$

对 $z_2$ 求导：

$$
\dot{z}_2 = \frac{\partial f_1}{\partial x_1}(x_1) \dot{x}_1 + \dot{x}_2
$$
$$
= \frac{\partial f_1}{\partial x_1}(x_1)[f_1(x_1) + x_2] + f_2(x_1, x_2) + u
$$

步骤 2：设计反馈输入

选择控制律：

$$
u = u_{nl}(x_1, x_2) + v
$$

其中非线性补偿项为：

$$
u_{nl}(x_1, x_2) = -\frac{\partial f_1}{\partial x_1}(x_1)[f_1(x_1) + x_2] - f_2(x_1, x_2)
$$

步骤 3：代入系统

代入后得到简化系统：

$$
\dot{x}_1 = z_2, \quad \dot{z}_2 = v
$$

这就是一个线性时不变系统（LTI System），
控制输入 $v$ 可以通过线性控制器（如 LQR 或 PID）来设计。

✅ 总结

步骤	含义
1️⃣ 系统分析	确定系统的非线性项 $f(x), g(x)$
2️⃣ 反馈设计	定义 $u = u_{nl}(x) + \beta(x)v$ 抵消非线性
3️⃣ 状态变换	构造线性等效模型
4️⃣ 控制设计	对 $v$ 使用线性控制方法

📘 一句话总结：

反馈线性化通过“补偿非线性 + 重新定义输入”，
将非线性系统等效转化为线性系统，
从而使复杂的机器人控制问题变得可分析、可设计、可实现。

📖 总结：

非线性系统虽普遍存在，但通过平衡点线性化与反馈线性化，
我们能利用线性控制理论的成熟工具，让复杂系统在局部范围内表现出可预测、可控的行为。

16. 稳定性分析（System Stability Analysis）

系统稳定性（System Stability）是控制理论中的核心概念，
它描述系统在受到扰动或输入信号时，是否能保持或回到平衡状态。

稳定性决定了机器人或任何动态系统能否在控制下正常工作。
例如，一个稳定的机械臂能在停止施加力矩后保持静止，
而一个不稳定的机械臂则可能持续震荡或偏离目标。

16.1 稳定性的概念（Concept of Stability）

定义：
若系统在有界输入（bounded input）下产生有界输出（bounded output），
则称该系统是BIBO 稳定（Bounded Input Bounded Output Stable）。

数学定义如下：

$$
|u(t)| < \infty \quad \Rightarrow \quad |y(t)| < \infty
$$

💡 为什么稳定性很重要（Why Stability Matters）

在机器人学中：

• 稳定的机器人能平稳移动、准确响应指令；
• 不稳定的机器人可能发生振荡、抖动或发散。

示例：

• 稳定：机械臂在停止施加力矩后保持位置；
• 不稳定：机械臂在停止控制后仍剧烈摆动。

16.2 稳定性的类型（Types of Stability）

稳定性可从不同角度定义与分析：

类型	依据	描述
BIBO 稳定性	输入输出关系	使用传递函数（Transfer Function）分析系统输出是否有界
内部稳定性（Internal Stability）	状态空间模型	通过状态矩阵的特征值分析系统内部状态是否收敛
李雅普诺夫稳定性（Lyapunov Stability）	能量函数（Energy Function）	适用于非线性系统，通过能量函数变化判断稳定性

我们在第17部分讨论BIBO

16.3 状态空间下的稳定性（Stability in State-Space）

对于状态空间方程：

$$
\dot{x}(t) = A x(t) + B u(t), \quad y(t) = C x(t) + D u(t)
$$

系统的稳定性取决于矩阵 $A$ 的特征值（Eigenvalues）。

判据（Criterion）

系统稳定当且仅当所有特征值的实部为负：

$$
\Re(\lambda_i(A)) < 0 \quad \forall i
$$

系统的稳定性取决于特征值在复平面上的位置，可以总结如下表所示：

特征值实部情况	系统类型	动态特征	稳定性描述
$\Re(\lambda_i) < 0$	渐近稳定（Asymptotically Stable）	指数衰减	状态随时间收敛到平衡点
$\Re(\lambda_i) = 0$	边界稳定（Marginally Stable）	持续振荡	不发散也不衰减，能量守恒
$\Re(\lambda_i) > 0$	不稳定（Unstable）	指数增长	状态随时间发散

示例解释：

• 若 $A = \begin{bmatrix}-2 & 0 \ 0 & -3\end{bmatrix}$，则 $\lambda = {-2, -3}$ → 稳定；
• 若 $A = \begin{bmatrix}1 & 0 \ 0 & -2\end{bmatrix}$，则 $\lambda = {1, -2}$ → 不稳定；
• 若 $\lambda = {0, -2}$，则边界稳定。

16.4 李雅普诺夫稳定性（Lyapunov Stability）

李雅普诺夫稳定性是分析非线性系统稳定性的基本方法，
核心思想是用一个能量函数 $V(x)$ 来判断系统状态随时间的变化。

🧠 直观理解（Explanation）

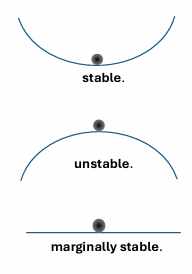
可以将系统状态想象为一个小球在不同地形上的运动：

• 在碗底（能量最低点） → 小球会滚回 → 稳定；
• 在山顶 → 轻微扰动即滚下 → 不稳定；
• 在平面上 → 停在原地但不会回到原点 → 边界稳定（Marginally Stable）。

📐 数学定义（Mathematical Definition）

对于非线性系统：

$$
\dot{x} = f(x), \quad x \in \mathbb{R}^n
$$

若平衡点在 $x = 0$，则系统在该点李雅普诺夫稳定当且仅当：

$$
\forall \epsilon > 0, \ \exists \delta > 0, \ \text{使得} \ ||x(0)|| < \delta \Rightarrow ||x(t)|| < \epsilon, \ \forall t \ge 0
$$

即：系统从接近平衡点出发后，始终保持在有限邻域内。

16.5 李雅普诺夫函数法（Lyapunov Function Method）

我们引入一个“能量型”函数 $V(x)$（称为李雅普诺夫函数）：

$$
V(x) > 0 \text{ for } x \ne 0, \quad V(0) = 0
$$

并计算其导数：

$$
\dot{V}(x) = \frac{dV}{dt}
$$

判断标准：

条件	稳定性类型
$\dot{V}(x) < 0$	渐近稳定（Asymptotically Stable）
$\dot{V}(x) = 0$	稳定（但非渐近）
$\dot{V}(x) > 0$	不稳定（Unstable）

💡 一维系统数值例子（1D Example）

考虑系统：

$$
\dot{x} = -x
$$

选择李雅普诺夫函数：

$$
V(x) = x^2
$$

计算导数：

$$
\dot{V}(x) = 2x\dot{x} = 2x(-x) = -2x^2 < 0
$$

因此，该系统是**渐近稳定（Asymptotically Stable）**的。

✅ 小结（Summary）

稳定性类型	分析依据	判据	应用场景
内部稳定性	状态矩阵 $A$ 特征值	$\Re(\lambda_i(A)) < 0$	线性状态空间系统
李雅普诺夫稳定性	能量函数 $V(x)$	$\dot{V}(x) < 0$	非线性系统、机器人控制

📘 一句话总结：

稳定性是控制系统的生命线。
线性系统依赖特征值判定稳定，非线性系统则依赖李雅普诺夫函数。
若系统能在扰动下回归平衡点，即可认为其“稳定”。

17. 传递函数与 BIBO 稳定性（Transfer Function and BIBO Stability）

17.1 传递函数（Transfer Function）

定义：
传递函数（Transfer Function）描述了系统输入与输出之间的数学关系，通常定义在 拉普拉斯域（Laplace Domain），适用于线性、时不变（LTI）系统。

其一般形式为：

$$
G(s) = \frac{Y(s)}{U(s)}
$$

其中：

• $U(s)$：输入信号的拉普拉斯变换；
• $Y(s)$：输出信号的拉普拉斯变换；
• $G(s)$：系统的传递函数。

📘 直观理解：
传递函数是系统的“频域指纹”，帮助我们分析稳定性、频率响应、动态特性等。

17.2 拉普拉斯变换（Laplace Transform）

定义：

拉普拉斯变换是一种将时域函数转换为**复频域函数（s 域）**的工具，用以简化微分方程求解。

$$
\mathcal{L}[f(t)] = F(s) = \int_0^{\infty} f(t)e^{-st}dt
$$

反变换为：

$$
\mathcal{L}^{(-1)}[F(s)] = f(t) = \frac{1}{2\pi j} \int_{c-j\infty}^{c+j\infty} F(s)e^{st}ds, \quad t>0
$$

🧭 意义：

拉普拉斯变换是连接“微分方程”与“传递函数”的桥梁。

17.3 拉普拉斯变换性质（Properties）

性质	数学表达	含义
线性性	$\mathcal{L}[a f(t) + b g(t)] = aF(s) + bG(s)$	可线性叠加
一阶微分	$\mathcal{L}[\dot{f}(t)] = sF(s) - f(0^+)$	导数变乘法
二阶微分	$\mathcal{L}[\ddot{f}(t)] = s^2 F(s) - s f(0^+) - \dot{f}(0^+)$	高阶导数扩展
积分	$\mathcal{L}\left[\int_0^t f(\tau)d\tau\right] = \frac{F(s)}{s}$	积分变除法
时移	$\mathcal{L}[f(t-T)] = e^{-sT}F(s)$	延迟产生指数项

17.4 初值与终值定理（Initial & Final Value Theorems）

定理	数学表达	说明
初值定理	$f(0^+) = \lim_{s\to\infty} sF(s)$	求瞬时响应初值
终值定理	$\lim_{t\to\infty} f(t) = \lim_{s\to 0} sF(s)$	求系统稳态响应

⚠️ 注意：
若系统不稳定（极点在右半平面），终值定理不适用。

17.5 BIBO 稳定性（Bounded Input – Bounded Output）

定义：
若系统在有界输入下产生有界输出，则称系统是 BIBO 稳定（Bounded Input Bounded Output Stable）：

$$
|u(t)| < \infty \Rightarrow |y(t)| < \infty
$$

基于传递函数的判据：

若系统传递函数为：

$$
G(s) = \frac{N(s)}{D(s)}
$$

系统的极点（Poles）定义为 $D(s) = 0$ 的根。

系统 BIBO 稳定的条件是：

$$
\Re(p_i) < 0 \quad \forall \text{极点 } p_i
$$

极点位置	系统状态	说明
所有极点在左半平面	稳定	响应指数衰减
极点在虚轴上	边界稳定	持续振荡
任意极点在右半平面	不稳定	响应发散

17.6 对比：BIBO vs 内部稳定（Internal Stability）

稳定性类型	基于	判据	适用系统
BIBO 稳定	输入输出关系	极点在左半平面	传递函数模型
内部稳定（State Stability）	状态空间	$\Re(\lambda_i(A)) < 0$	状态空间模型
Lyapunov 稳定	能量函数	$\dot{V}(x) < 0$	非线性系统

📘 总结：

传递函数与拉普拉斯变换为我们提供了从“时域”到“频域”的分析工具。

BIBO 稳定性判据帮助我们通过极点位置快速判断系统是否在外部输入下保持稳定。

18. 非线性状态空间模型（Nonlinear State Model）

18.1 状态方程的定义（State Equations）

考虑一个具有 $n$ 个状态变量、$m$ 个输入变量的非线性系统：

$$
\begin{cases}
\dot{x}_1 = f_1(t, x_1, \ldots, x_n, u_1, \ldots, u_m) \
\dot{x}_2 = f_2(t, x_1, \ldots, x_n, u_1, \ldots, u_m) \
\vdots \
\dot{x}_n = f_n(t, x_1, \ldots, x_n, u_1, \ldots, u_m)
\end{cases}
$$

其中：

• $u_1, u_2, \ldots, u_m$：输入变量（Input Variables）
• $x_1, x_2, \ldots, x_n$：状态变量（State Variables）
• $\dot{x}_i = \dfrac{dx_i}{dt}$：状态变量的时间导数

📘 意义说明：

非线性状态方程用于描述系统的内部动态，
每个状态变量的变化率取决于系统的当前状态和输入。

18.2 向量形式（Vector Form）

将状态和输入写成向量形式：

$$
x =
\begin{bmatrix}
x_1 \ x_2 \ \vdots \ x_n
\end{bmatrix},
\quad
u =
\begin{bmatrix}
u_1 \ u_2 \ \vdots \ u_m
\end{bmatrix},
\quad
f(t, x, u) =
\begin{bmatrix}
f_1(t, x, u) \ f_2(t, x, u) \ \vdots \ f_n(t, x, u)
\end{bmatrix}.
$$

于是系统可写为紧凑形式：

$$
\dot{x} = f(t, x, u)
$$

📘 直观理解：

向量形式使得系统分析更方便，
它是非线性控制系统研究的标准表示形式。

18.3 输出方程与特殊形式（Output Equation & Special Cases）

引入输出映射函数：

$$
\dot{x} = f(t, x, u), \quad y = h(t, x, u)
$$

其中 $y$ 为系统输出。

特殊情况（Special Cases）：

系统类型	数学形式	特点
线性时变系统（LTV）	$\dot{x} = A(t)x + B(t)u,\quad y = C(t)x + D(t)u$	系数随时间变化，但系统仍为线性
无输入系统（Unforced System）	$\dot{x} = f(t, x)$	系统仅由内部状态驱动
自治系统（Autonomous System）	$\dot{x} = f(x)$	不显含时间或外部输入
时不变系统（Time-Invariant System）	$\dot{x} = f(x, u), ; y = h(x, u)$	若输入波形整体平移，系统响应轨迹仅发生时间平移

18.4 时不变性的含义（Meaning of Time Invariance）

定义：
若将初始时间从 $t_0$ 平移至 $t_0 + a$，并施加相同的输入波形（但时间也相应平移），
系统轨迹保持不变（仅时间平移），则系统为时不变系统（Time-Invariant System）。

$$
f(t, x, u) = f(x, u) \quad \Rightarrow \quad \text{系统不随时间变化}
$$

📘 直观理解：

时不变系统意味着系统的规律不会随时间变化，
相同的输入模式在不同时间施加，产生的响应只是延迟而非变化。

✅ 总结

分类	方程形式	是否含时间	是否含输入	举例
自治系统（Autonomous）	$\dot{x} = f(x)$	❌	❌	单摆系统（无控制力）
时不变系统（Time-Invariant）	$\dot{x} = f(x, u)$	❌	✅	线性电路
时变系统（Time-Varying）	$\dot{x} = f(t, x, u)$	✅	✅	参数随时间变化的控制系统
无输入系统（Unforced）	$\dot{x} = f(t, x)$	✅	❌	自然衰减系统

📘 一句话总结：

非线性状态模型统一了各种动力系统的数学表达，是理解线性化与控制设计的基础。

19. 解的存在与唯一性（Existence and Uniqueness of Solutions）

19.1 基本形式（Fundamental Form）

对于系统：

$$
\dot{x} = f(t, x)
$$

我们关心的是：
是否存在解？以及解是否唯一？

这依赖于 $f(t, x)$ 的连续性与 利普希茨（Lipschitz）条件。

19.2 条件 1：分段连续性（Piecewise Continuity）

为了保证微分方程的解能够“存在”，
我们首先要求 $f(t, x)$ 对时间 $t$ 的变化是分段连续的（piecewise continuous）。

• 这意味着在任意有限时间区间 $J_0 \subset J$ 内，
  函数 $f(t, x)$ 关于时间 $t$ 是连续的，
  只允许在有限个时间点出现跳变（例如切换控制、冲击输入等）。

📘 直观理解：

系统的右端项不能“乱跳”太多，只能有有限次不连续。
比如，开关电路或机器人控制中有限次模式切换的系统，都属于分段连续系统。

19.3 条件 2：局部 Lipschitz 连续性（Locally Lipschitz in $x$）

为了保证解的唯一性（uniqueness），
我们要求 $f(t, x)$ 在状态变量 $x$ 上满足 局部 Lipschitz 连续性。

定义如下：
存在某个邻域

$$
N(x_0, r) = { x \in \mathbb{R}^n \mid |x - x_0| < r }
$$

以及一个常数 $L > 0$，
使得对该邻域中的任意两个点 $x, y$，都有：

$$
|f(t, x) - f(t, y)| \le L |x - y|
$$

则称 $f(t, x)$ 在 $x_0$ 处 局部 Lipschitz（locally Lipschitz）。

📘 几何意义：

在小范围内，$f(t, x)$ 的变化不会比直线变化更剧烈。
也就是说，函数曲线的“斜率”被某个常数 $L$ 限制住了。

📘 直观理解：

如果系统方程对状态变量变化得太“陡”（例如无穷大斜率或断点），
那么解的轨迹可能会分叉或不唯一。
局部 Lipschitz 条件保证了系统在局部区域内的“可预测性”。

19.4 进一步定义与判定准则（Further Definitions and Characterization）

为了在数学上更准确地刻画 Lipschitz 连续性，我们需要引入一些更一般的定义与判定方法。

📘 解释：
局部 Lipschitz 意味着函数在每个点附近变化率是“可控的”，但这个控制常数 $L$ 可以随位置变化。

一维情况（When $ n = 1 $）

当 $f$ 仅依赖于一个变量 $x$ 时，存在常数 $L > 0$，使得：

$$
\frac{|f(y) - f(x)|}{|y - x|} \le L, \quad \forall x, y \in I
$$

这意味着函数曲线上任意两点连线的斜率绝对值都有上界。

📘 几何意义：

在 $f(x)$ 的图像上，任意局部区域内的曲线斜率不会“无限大”，
从而保证函数图像的光滑性和解的可预测性。

通过导数的判定（Characterization via Derivatives）

• 若 $f’(x)$ 在某点 $x_0$ 连续，则 $f(x)$ 在该点局部 Lipschitz。
  因为在 $x_0$ 附近 $|f’(x)|$ 有界，可以取常数 $L = k$ 使：

$$
|f(y) - f(x)| \le \sup_{\xi \in [x, y]} |f’(\xi)| , |y - x| \le k |y - x|
$$

• 推广到多维情况：

设 $t \in J \subset \mathbb{R}$ 且 $x \in D \subset \mathbb{R}^n$，
若 $f(t, x)$ 及其偏导数 $\frac{\partial f_i}{\partial x_j}$ 在 $J \times D$ 上连续，
则 $f(t, x)$ 在 $x$ 上是局部 Lipschitz。

📘 结论：

连续的一阶偏导数（$\mathcal{C}^1$ 函数） ⇒ 必然是局部 Lipschitz。
换言之，只要函数在局部区域内“可微且导数连续”，
就能保证系统解的存在与唯一性。

局部与全局 Lipschitz 的区别

类型	数学定义	特征	是否保证解唯一	示例
局部 Lipschitz	$\forall x_0, \exists L(x_0)$ 使 $|f(x) - f(y)| \le L(x_0)|x - y|$	只在小范围内约束	✅ 局部唯一	$f(x) = x^2$
全局 Lipschitz	存在全局常数 $L$ 对所有 $x, y$ 成立	全局约束变化率	✅ 全局唯一	$f(x) = -x$
非 Lipschitz	不满足连续导数或存在无穷斜率	变化率不可控	❌ 可能多解	$f(x) = x^{1/3}$

非 Lipschitz 例子与直观解释

• 不连续函数：
  若 $f(x)$ 在某点不连续，则该点不可能是局部 Lipschitz。

• 示例：
  $f(x) = x^{1/3}$ 在 $x = 0$ 处不是局部 Lipschitz，因为：

$$
f’(x) = \frac{1}{3}x^{-2/3} \to \infty \quad \text{当 } x \to 0
$$

• 解释：
  在 $x = 0$ 附近，函数斜率变得无限大，意味着系统对初始条件极端敏感，
  解可能出现分叉或不唯一。

19.5 定理（Lemma 1：存在与唯一性）

若 $f(t, x)$ 在 $t$ 上分段连续，并在 $x$ 上于 $x_0$ 局部 Lipschitz，
则存在 $\delta > 0$ 使得初值问题：

$$
\dot{x} = f(t, x), \quad x(t_0) = x_0
$$

在区间 $[t_0, t_0 + \delta]$ 上存在唯一解。

为什么 Lipschitz 条件重要？

• 若没有 Lipschitz 条件，唯一性无法保证。
  例如：

$$
\dot{x} = x^{1/3}, \quad x(0) = 0
$$

有两个解：

$$
x(t) \equiv 0, \quad x(t) = \left(\frac{2t}{3}\right)^{3/2}
$$

19.6 有限逃逸时间（Finite Escape Time）

示例：

$$
\dot{x} = -x^2, \quad x(0) = -1
$$

求得：

$$
x(t) = \frac{1}{t - 1}, \quad x(t) \to -\infty \text{ 当 } t \to 1
$$

📘 结论：
此解在 $t = 1$ 处发生有限时间逃逸（finite escape time）。

一般情况（Remark）：

若 $f(t, x)$ 在区域 $D$ 上局部 Lipschitz，
且 $\dot{x} = f(t, x)$ 的解存在有限逃逸时间 $t_e$，
则当 $t \to t_e$，轨迹 $x(t)$ 必离开 $D$ 的任意紧子集。

19.7 全局 Lipschitz 连续性（Globally Lipschitz in $x$）

若存在常数 $L > 0$，对所有 $x, y \in \mathbb{R}^n$ 恒有：

$$
|f(t, x) - f(t, y)| \le L |x - y|
$$

则称 $f(t, x)$ 在 $x$ 上 全局 Lipschitz（globally Lipschitz）。

判定方式（Characterization via Partials）

若 $f(t, x)$ 及其偏导数 $\partial f_i / \partial x_j$ 在所有 $x \in \mathbb{R}^n$ 上连续，
则当且仅当所有偏导数全局有界时，$f(t, x)$ 全局 Lipschitz。

示例（Example）

$$
f(x) = -x^2
$$

• 局部 Lipschitz ✅ （在每个有限区间内成立）
• 全局 Lipschitz ❌ （因为 $f’(x) = -2x$ 非全局有界）

✅ 总结表

类型	数学定义	是否唯一解	示例
局部 Lipschitz	$|f(x) - f(y)| \le L|x - y|$ 在邻域内成立	仅局部保证	$f(x)=x^{1/3}$（不满足）
全局 Lipschitz	对所有 $x,y$ 成立	全局唯一解	$f(x)=-x$
非 Lipschitz	不连续或斜率无界	唯一性丧失	$f(x)=x^{1/3}$
有限逃逸	解有限时间发散	轨迹离开有界域	$f(x)=-x^2$

📘 一句话总结：

若 $f(t, x)$ 满足分段连续性与局部 Lipschitz 条件，则系统的解在某个时间区间内存在且唯一；
若进一步满足全局 Lipschitz，则解在整个定义域内唯一且连续存在。

20. 平衡点与相平面分析（Equilibrium and Phase Plane Analysis）

20.1 平衡点定义（Equilibrium Point Definition）

对于系统：

$$
\dot{x} = f(t, x)
$$

若存在一个常数向量 $x^*$ 满足：

$$
x(t_0) = x^* \Rightarrow x(t) \equiv x^*, \quad \forall t \ge t_0
$$

则称 $x^*$ 为系统的平衡点（equilibrium point）。

📘 直观理解：

当系统处于平衡点时，其状态不再随时间变化，即 $\dot{x}=0$，系统“静止”。

Autonomous 情况（自治系统）

对于自治系统（不显含时间）：

$$
\dot{x} = f(x)
$$

平衡点由下式给出：

$$
f(x) = 0
$$

平衡点的类型

• 平衡点可以是孤立的（isolated），即单独存在；
• 也可以构成连续集（continuum），如一条线或一个面上的点都满足 $f(x)=0$。

📘 例子：

简单摆系统在最低点和平衡位置（垂直向下）是孤立平衡点，
而一个滑块在水平面上静止的所有位置则形成连续平衡态。

20.2 二维自治系统（Planar Autonomous System）

考虑一个二维系统：

$$
\begin{cases}
\dot{x}_1 = f_1(x_1, x_2) \
\dot{x}_2 = f_2(x_1, x_2)
\end{cases}
$$

系统的瞬时速度向量为：

$$
\vec{v}(x_1, x_2) = \big(f_1(x_1, x_2), , f_2(x_1, x_2)\big)
$$

该向量场（vector field）描述了系统在状态空间中的运动方向与速率。

20.3 零流线（Nullclines）

• $x_1$-nullcline：
  当 $f_1(x_1, x_2)=0$ 时，$\dot{x}_1 = 0$，
  系统在该线上竖直流动（上下运动）。

• $x_2$-nullcline：
  当 $f_2(x_1, x_2)=0$ 时，$\dot{x}_2 = 0$，
  系统在该线上水平流动（左右运动）。

• 交点：
  满足 $f_1 = f_2 = 0$ 的点即为平衡点（equilibria）。

📘 几何解释：

零流线是状态变量“速度为零”的集合，
它们的交点对应系统在状态空间中的静止状态。

20.4 等斜率线（Isoclines, Constant-Slope Lines）

沿着系统轨迹：

$$
\frac{dx_2}{dx_1} = \frac{\dot{x}_2}{\dot{x}_1} = \frac{f_2(x_1, x_2)}{f_1(x_1, x_2)} = m
$$

若给定常数斜率 $m$，则有：

$$
f_2(x_1, x_2) = m f_1(x_1, x_2)
$$

称这些曲线为等斜率线（isoclines），
表示系统在相空间中方向相同的流动轨迹。

📘 应用：

等斜率线常用于手工绘制相平面图，只需绘制少量等斜率线，就能近似看出系统流场的方向分布。
可以帮助分析系统的动态行为，例如流向、稳定性与震荡趋势。

20.5 相平面方法总结（Phase Plane Overview）

概念	数学定义	几何意义	作用
平衡点	$f(x)=0$	静止点	分析稳定性
零流线（Nullcline）	$f_i(x)=0$	变量速度为零的轨迹	确定平衡点位置
等斜率线（Isocline）	$f_2 = m f_1$	相同方向的轨迹	近似流场方向
向量场（Vector Field）	$(f_1, f_2)$	流动方向	描述系统运动状态

📘 一句话总结：

平衡点是系统的“静止状态”，零流线和等斜率线帮助我们可视化系统的流动趋势，
从而通过相平面方法判断系统的稳定性与动态特征。

21. 平面线性系统与平衡点附近的行为（Linear Systems in the Plane & Behavior Near Equilibria）

21.1 平面线性系统的形式（Form of a Linear System）

考虑二维线性系统：

$$
\dot{x} = A x, \quad A \in \mathbb{R}^{2\times2}
$$

存在一个可逆矩阵 $M$ 使得：

$$
x(t) = M e^{Jt} M^{-1} x_0
$$

其中 $J$ 为 $A$ 的实 Jordan 标准形（real Jordan form）：

$$
J =
\begin{bmatrix}
\lambda_1 & 0 \
0 & \lambda_2
\end{bmatrix}
\quad \text{或} \quad
J =
\begin{bmatrix}
\alpha & -\beta \
\beta & \alpha
\end{bmatrix}
$$

若定义 $z = M^{-1}x$，则系统变为：

$$
\dot{z} = Jz
$$

此时系统被“解耦”，每个方向独立描述不同的动力学行为。

21.2 情况一：两个实特征值（Case I: Two Real Eigenvalues）

若 $A v_i = \lambda_i v_i$，其中 $(\lambda_1, v_1), (\lambda_2, v_2)$ 为实特征对，则：

$$
\dot{z}_1 = \lambda_1 z_1, \quad \dot{z}_2 = \lambda_2 z_2
$$

因此：

$$
z_1(t) = z_{10} e^{\lambda_1 t}, \quad
z_2(t) = z_{20} e^{\lambda_2 t}
$$

消去 $t$ 得到轨迹方程：

$$
z_2 = C z_1^{\lambda_2 / \lambda_1}, \quad C = z_{20} / z_{10}^{\lambda_2 / \lambda_1}
$$

系统的相图形状取决于 $\lambda_1$ 和 $\lambda_2$ 的符号。

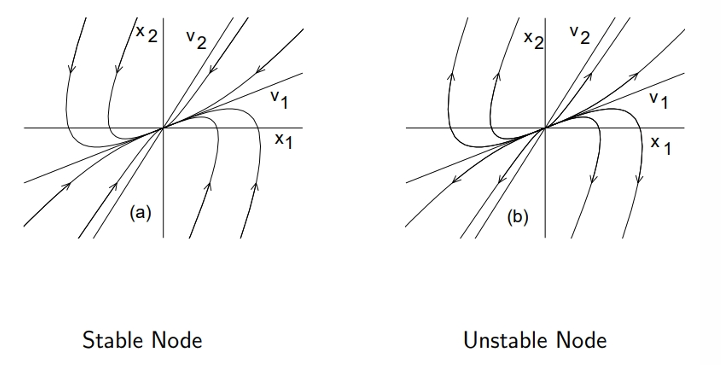
(1) 当 $\lambda_2 < \lambda_1 < 0$ 时 —— 稳定节点（Stable Node）

• 两个指数项 $e^{\lambda_1 t}$、$e^{\lambda_2 t}$ 均 $\to 0$；
• $\lambda_2$ 的衰减更快，称为 快特征值（fast eigenvalue）；
• $\lambda_1$ 对应 慢特征方向（slow eigenvector）。

轨迹方程（消去 $t$）：
$$
z_2 ;=; c, z_1^{\lambda_2/\lambda_1}, \qquad \frac{\lambda_2}{\lambda_1} > 1 .
$$

→ 解随时间单调收敛，所有轨迹指向平衡点（原点），沿慢特征方向“拉长”。

（2）当 $0 < \lambda_1 < \lambda_2$ 时 —— 不稳定节点（Unstable Node）

• 两个指数项 $e^{\lambda_1 t}$、$e^{\lambda_2 t}$ 均 $\to \infty$；
• $\lambda_2$ 增长更快，是 快不稳定特征值；$\lambda_1$ 为 慢不稳定特征值；
• 轨迹从原点沿特征方向向外发散。

同样有轨迹方程：
$$
z_2 ;=; c, z_1^{\lambda_2/\lambda_1}, \qquad \frac{\lambda_2}{\lambda_1} > 1 .
$$

区别在于：对稳定节点 $t !\to! +\infty$ 时 $z !\to! 0$；
而对不稳定节点，$t !\to! +\infty$ 时 $z !\to! \infty$。
→ 相图上所有轨迹自原点“喷出”，并在快特征方向上扩张更显著。

(3) 当 $\lambda_2 < 0 < \lambda_1$ 时 —— 鞍点（Saddle Point）

在这种情况下，系统存在一个稳定方向和一个不稳定方向：

• $e^{\lambda_1 t} \to \infty$，沿特征向量 $v_1$ 的方向发散（不稳定方向）；
• $e^{\lambda_2 t} \to 0$，沿特征向量 $v_2$ 的方向收敛（稳定方向）。

我们称：

• $\lambda_2$ 为 稳定特征值（stable eigenvalue），对应 稳定特征向量 $v_2$；
• $\lambda_1$ 为 不稳定特征值（unstable eigenvalue），对应 不稳定特征向量 $v_1$。

轨迹方程为：
$$
z_2 = c , z_1^{\lambda_2 / \lambda_1}, \quad \frac{\lambda_2}{\lambda_1} < 0
$$

由此可以看出：

• 部分轨迹（沿 $v_2$）随着时间收敛至原点；
• 其余轨迹（沿 $v_1$）则会随时间发散离开原点。

因此，系统的相图呈现典型的 鞍形结构（saddle pattern）：
原点是平衡点，但仅在稳定流形（stable manifold）上局部吸引，其余方向上均发散。

📘 总结：

鞍点系统既包含“吸引”又包含“排斥”特征。
平衡点在某方向稳定、另一方向不稳定，
因此轨迹会沿稳定方向被吸引，同时沿不稳定方向被推离。

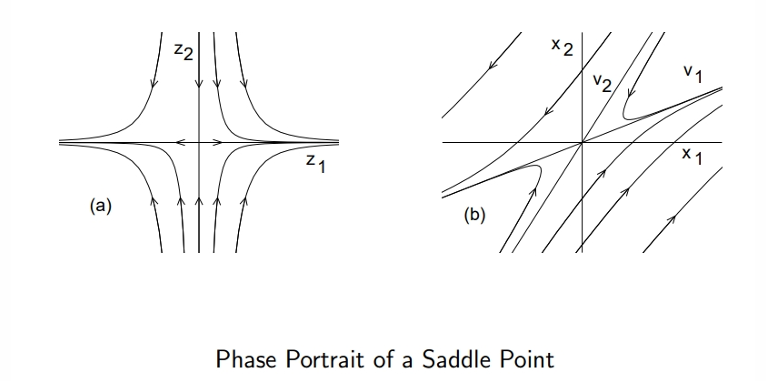
21.3 情况二：复特征值（Case II: Complex Conjugate Eigenvalues）

若特征值为共轭对：

$$
\lambda_{1,2} = \alpha \pm j \beta, \quad \beta \ne 0
$$

则系统为：

$$
\begin{cases}
\dot{z}_1 = \alpha z_1 - \beta z_2 \
\dot{z}_2 = \beta z_1 + \alpha z_2
\end{cases}
$$

转化为极坐标形式：

$$
r = \sqrt{z_1^2 + z_2^2}, \quad \theta = \tan^{-1}(z_2/z_1)
$$

得到：

$$
r(t) = r_0 e^{\alpha t}, \quad \theta(t) = \theta_0 + \beta t
$$

• $\alpha < 0$ → $r(t) \to 0$ → 稳定焦点（stable focus）
• $\alpha > 0$ → $r(t) \to \infty$ → 不稳定焦点（unstable focus）
• $\alpha = 0$ → $r(t)$ 恒定 → 中心（center）

📘 几何解释：

当系统存在复特征值时，轨迹绕平衡点旋转，形成螺旋或圆形轨迹，
旋转角速度由 $\beta$ 决定，收敛或发散速度由 $\alpha$ 决定。

21.4 平衡点附近系统的行为（Behavior Near Equilibria）

非线性系统在平衡点附近的定性行为（qualitative behavior）
往往与对应线性系统相似，因此可通过线性化（linearization）分析。

$$
\dot{x} = f(x), \quad f(x^*) = 0
$$

在平衡点 $x^*$ 附近展开一阶泰勒近似：

$$
\dot{x} \approx A(x - x^), \quad A = \frac{\partial f}{\partial x}\bigg|_{x=x^}
$$

此处的 $A$ 即为 Jacobian 矩阵（雅可比矩阵）。
系统局部行为取决于 $A$ 的特征值。

21.5 平衡点分类总结表（Classification of Equilibria）

特征值形式	平衡点类型	稳定性	轨迹形状
$\lambda_1, \lambda_2 < 0$	稳定节点 (Stable Node)	渐近稳定	所有轨迹收敛到原点
$\lambda_1, \lambda_2 > 0$	不稳定节点 (Unstable Node)	不稳定	所有轨迹发散
$\lambda_1 < 0 < \lambda_2$	鞍点 (Saddle)	不稳定	一部分收敛，一部分发散
$\lambda_{1,2} = \alpha \pm j\beta$, $\alpha<0$	稳定焦点 (Stable Focus)	渐近稳定	螺旋收敛
$\lambda_{1,2} = \alpha \pm j\beta$, $\alpha>0$	不稳定焦点 (Unstable Focus)	不稳定	螺旋发散
$\lambda_{1,2} = j\beta$	中心 (Center)	稳定（但不渐近）	闭合圆轨迹

📘 总结：

线性系统的特征值决定了其平衡点的类型与稳定性。
对非线性系统，可通过线性化近似，使用雅可比矩阵的特征值判断其局部动力学行为。

22. Linearization Around an Equilibrium

Linearization（线性化） 是在系统平衡点附近，用一阶泰勒展开将非线性系统近似为线性系统的过程。
其核心思想是：

在平衡点附近，系统的行为可以通过雅可比矩阵（Jacobian matrix）所定义的线性系统来描述。

22.1 非线性系统形式（Nonlinear System Form）

考虑一个二维非线性系统：
$$
\dot{x}_1 = f_1(x_1, x_2), \quad
\dot{x}_2 = f_2(x_1, x_2)
$$

设 $(p_1, p_2)$ 是系统的平衡点，即：
$$
f_1(p_1, p_2) = 0, \quad f_2(p_1, p_2) = 0
$$

22.2 泰勒展开与线性近似（Taylor Expansion & Local Approximation）

在平衡点 $(p_1, p_2)$ 处展开一阶泰勒级数：
$$
\dot{x}_1 = f_1(p_1, p_2) + a_{11}(x_1 - p_1) + a_{12}(x_2 - p_2) + \text{H.O.T.},
$$

$$
\dot{x}_2 = f_2(p_1, p_2) + a_{21}(x_1 - p_1) + a_{22}(x_2 - p_2) + \text{H.O.T.}
$$

其中 H.O.T.（Higher Order Terms） 表示高阶项，在局部线性化分析中通常忽略。

22.3 雅可比矩阵（Jacobian Matrix）

系数矩阵 $A = [a_{ij}]$ 定义为系统在平衡点处的雅可比矩阵：

$$
A = [a_{ij}] =
\left[
\frac{\partial f_i}{\partial x_j}
\right]\Big|_{x = p}
$$

展开形式为：

$$
A =\begin{pmatrix}
a_{11} & a_{12} \
a_{21} & a_{22}
\end{pmatrix}=\begin{pmatrix}
\dfrac{\partial f_1}{\partial x_1} & \dfrac{\partial f_1}{\partial x_2} \
\dfrac{\partial f_2}{\partial x_1} & \dfrac{\partial f_2}{\partial x_2}
\end{pmatrix}\Big|_{x = p}
$$

22.4 局部坐标变换（Local Coordinates）

定义偏移变量：
$$
y_1 = x_1 - p_1, \quad y_2 = x_2 - p_2
$$

向量形式表示为：
$$
y = (y_1, y_2)^\top
$$

代入后，线性化系统变为：
$$
\dot{y} = A y
$$

22.5 符号说明（Variable Explanation）

符号	含义	说明
$x_1, x_2$	状态变量	系统的动态状态（如位置、速度等）
$f_1, f_2$	非线性函数	定义系统的动力学关系
$(p_1, p_2)$	平衡点	满足 $\dot{x} = 0$ 的点
$A$	雅可比矩阵	系统在平衡点处的线性近似矩阵
$a_{ij}$	雅可比元素	$a_{ij} = \dfrac{\partial f_i}{\partial x_j}$
$y_1, y_2$	局部偏移变量	表示状态相对于平衡点的偏移
$\text{H.O.T.}$	高阶项	在线性化过程中被忽略的高阶非线性项

22.6 局限性（Limitations of Linearization）

• 线性化是局部一阶近似，仅在平衡点附近有效；
• 无法反映系统的全局非线性行为；
• 某些动力学现象（如极限环、混沌）仅在非线性系统中出现，线性模型无法捕捉。

22.7 非线性现象（Nonlinear Phenomena）

现象	描述
有限逃逸时间（Finite Escape Time）	状态变量在有限时间内趋于无穷大
多个平衡点（Multiple Equilibria）	系统可能具有多个孤立平衡解
极限环（Limit Cycle）	状态沿闭合轨迹周期运动
次谐波或近周期振荡（Subharmonic，harmonic，or almost-periodic oscillations）	出现与驱动频率非整数倍关系的振荡
混沌（Chaos）	对初值敏感、非周期且复杂的行为
多模态行为（Multiple Modes）	不同区域呈现不同动力学模式

📘 总结：

线性化是分析非线性系统局部稳定性与动态特性的关键工具，
它将复杂的非线性方程在平衡点附近简化为可解析的线性形式。
然而，它仅能描述局部行为，不能替代完整的非线性动力学分析。

23. 极限环（Limit Cycles）

23.1 引言（Introduction）

在非线性系统中，除了平衡点（Equilibrium Point）之外，还存在一种自激振荡现象：
系统的状态会在相平面上形成封闭轨迹并周期性运动。
这种封闭轨迹被称为 极限环（Limit Cycle）。

极限环是一种孤立的封闭轨迹，其周围的轨迹要么向其收敛（稳定极限环），
要么远离它发散（不稳定极限环）。

23.2 范德波尔振子（Van der Pol Oscillator）

考虑一个经典的二阶非线性系统：

$$
\dot{x}_1 = x_2, \qquad
\dot{x}_2 = -x_1 + \varepsilon(1 - x_1^2)x_2
$$

其中参数 $\varepsilon > 0$ 控制系统的非线性与阻尼程度：

• 当 $\varepsilon$ 很小时，系统接近线性，表现为轻微阻尼振荡；
• 当 $\varepsilon$ 增大时，非线性效应显著，系统产生自维持振荡。

23.3 相图分析（Phase Portrait Analysis）

下图展示了不同 $\varepsilon$ 值下系统的相平面行为：

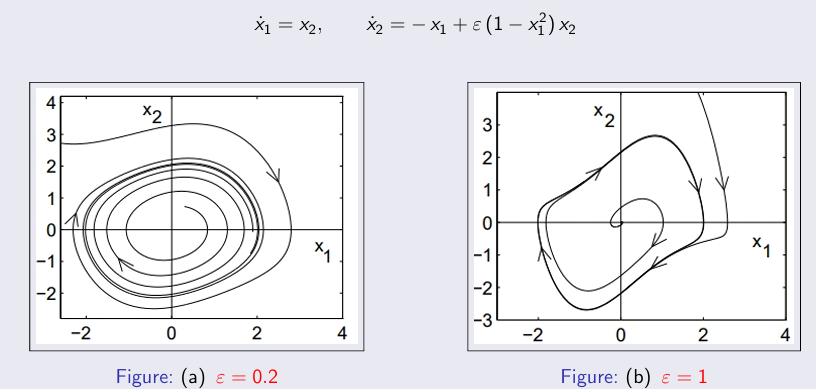
• 图 (a)：$\varepsilon = 0.2$，轨迹逐渐向内收敛，形成近似椭圆的封闭轨迹；
• 图 (b)：$\varepsilon = 1$，非线性阻尼增强，轨迹收敛至一个稳定的封闭曲线（极限环）。

$$
\text{Figure (a): } \varepsilon = 0.2 \qquad
\text{Figure (b): } \varepsilon = 1
$$

这些封闭曲线的存在说明系统在经历短暂的过渡后，进入稳定的周期运动状态。

23.4 极限环的数学特征（Mathematical Property）

对于极限环 $\Gamma$，存在周期 $T > 0$ 使得：

$$
x(t + T) = x(t), \quad \forall t
$$

并且在 $\Gamma$ 周围的邻域内，轨迹的渐近行为满足：

• 若轨迹趋向于 $\Gamma$：称为 稳定极限环（Stable Limit Cycle）；
• 若轨迹远离 $\Gamma$：称为 不稳定极限环（Unstable Limit Cycle）。

下图展示了两种典型情形：

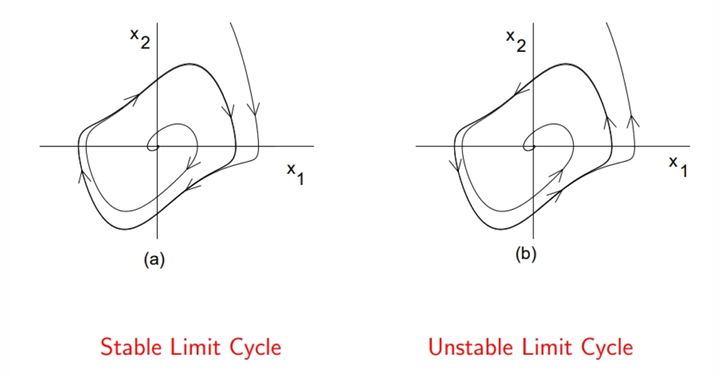
$$
\text{(a) 稳定极限环} \qquad \text{(b) 不稳定极限环}
$$

23.5 变量变换与奇异摄动（Slow–Fast System Form）

当 $\varepsilon$ 很大时，可通过变量变换简化系统行为：

$$
\dot{z}_1 = \frac{1}{\varepsilon}z_2, \qquad
\dot{z}_2 = -\varepsilon\left(z_1 - z_2 + \frac{1}{3}z_2^3\right)
$$

此时系统分为快变量（Fast Variable） 与 慢变量（Slow Variable）：

• 快变量决定轨迹的跳跃与突变；
• 慢变量决定轨迹沿“慢流形”的缓慢爬升。

这类系统被称为 慢–快系统（Slow–Fast System），广泛应用于神经振荡与电子电路建模。

23.6 小结（Summary）

概念	说明
极限环（Limit Cycle）	非线性系统中的孤立封闭轨迹
稳定极限环	周围轨迹逐渐收敛到该轨迹
不稳定极限环	周围轨迹远离该轨迹发散
范德波尔方程	展示极限环存在的典型非线性系统
慢–快系统形式	在 $\varepsilon$ 很大时的等价形式，用于分析快跳变与慢演化

📘 总结：

极限环是非线性系统独有的稳定振荡现象，
它揭示了系统在没有外部激励时仍能产生自维持周期运动的本质。
范德波尔振子为研究极限环、振荡与混沌等非线性行为奠定了理论基础。

24. 平衡点与 Lyapunov 稳定性（Stability of Equilibrium Points）

24.1 平衡点的定义（Equilibrium Point）

考虑一个自治系统：

$$
\dot{x} = f(x)
$$

🔹 定义

若存在某点 $x^*$ 满足：

$$
f(x^*) = 0
$$

则称该点为系统的平衡点（Equilibrium Point）。

🔹 解释

• 若系统状态从 $x(0) = x^*$ 开始，则由于 $\dot{x} = 0$，系统保持静止：
  $$
  x(t) \equiv x^*, \quad \forall t \ge 0
  $$
• 因此，平衡点代表系统的稳态解。

🔹 示例

例如一维系统 $\dot{x} = -x$，有 $f(x) = -x$，
则 $f(0) = 0$，因此 $x^* = 0$ 是平衡点。

24.2 稳定性的定义（Definition of Stability）

考虑系统 $\dot{x} = f(x)$ 的平衡点 $x = 0$。

（1）稳定（Stable）

若对于任意小的 $\varepsilon > 0$，存在 $\delta = \delta(\varepsilon) > 0$，
使得只要初始条件满足 $|x(0)| < \delta$，系统轨迹始终保持在 $\varepsilon$ 半径的邻域内：

$$
|x(0)| < \delta \Rightarrow |x(t)| < \varepsilon, \quad \forall t \ge 0
$$

则称该平衡点是稳定的。

👉 直观理解：
初始条件的微小扰动不会让系统远离平衡点。

（2）不稳定（Unstable）

若存在任意小的扰动导致系统轨迹发散（离开平衡点邻域），
则称平衡点不稳定。

（3）渐近稳定（Asymptotically Stable）

如果系统既稳定，且随着时间推移系统轨迹最终收敛到平衡点：

$$
\lim_{t \to \infty} x(t) = 0
$$

则称系统渐近稳定。

👉 直观解释：
不仅不会发散，还能“自动回到”平衡点，就像摆球最终停在最低点。

24.3 吸引域（Region of Attraction）

若原点是渐近稳定的平衡点，则定义：

（1）吸引域定义

所有使系统解收敛到平衡点的初始状态 $x_0$ 的集合：

$$
\mathcal{R} = { x_0 \in D \mid \lim_{t \to \infty} x(t; x_0) = 0 }
$$

称为吸引域（Region of Attraction）。

（2）全局渐近稳定（Global Asymptotic Stability）

若吸引域为整个 $\mathbb{R}^n$，即无论初始状态在哪，系统最终都回到平衡点：
$$
\mathcal{R} = \mathbb{R}^n
$$
则称该平衡点全局渐近稳定。

24.4 线性系统的稳定性（LTI Stability via Eigenvalues）

考虑线性系统：
$$
\dot{x} = A x
$$
其解为：
$$
x(t) = e^{At} x(0)
$$

若矩阵 $A$ 的所有特征值 $\lambda_i$ 满足：
$$
\Re(\lambda_i) < 0, \quad \forall i
$$
则系统渐近稳定。

若 $\Re(\lambda_i) = 0$，还需判断其代数重数和几何重数相等，否则系统发散。

24.5 指数稳定性（Exponential Stability）

（1）定义

若存在常数 $k \ge 1$、$\lambda > 0$、$c > 0$，使得：
$$
|x(t)| \le k |x(0)| e^{-\lambda t}, \quad \forall t \ge 0, \ |x(0)| < c
$$
则称系统在原点指数稳定（Exponentially Stable）。

（2）解释

• 系统的收敛速度与 $e^{-\lambda t}$ 成比例；
• $\lambda$ 越大，收敛越快；
• 若对任意初始条件成立，则为全局指数稳定。

（3）关系总结

$$
\text{指数稳定} \Rightarrow \text{渐近稳定}
$$
但反之不成立。

24.6 示例：非指数稳定系统

考虑：
$$
\dot{x} = -x^3
$$
解析解：
$$
x(t) = \frac{x(0)}{\sqrt{1 + 2t x(0)^2} }
$$

（1）渐近性判断

当 $t \to \infty$：
$$
x(t) \to 0
$$
故系统渐近稳定。

（2）指数性检验

假设指数稳定，则应存在常数 $k, \lambda > 0$，使得：
$$
|x(t)| \le k e^{-\lambda t} |x(0)|
$$

代入解析解：
$$
\frac{|x(0)|}{\sqrt{1 + 2t x(0)^2} } \le k e^{-\lambda t}|x(0)|
$$
化简得：
$$
\frac{e^{2\lambda t} }{1 + 2t x(0)^2} \le k^2
$$

但当 $t \to \infty$ 时：
$$
\frac{e^{2\lambda t} }{1 + 2t x(0)^2} \to \infty
$$

出现矛盾，故系统 仅渐近稳定，而非指数稳定。

24.7 Lyapunov 稳定性函数（Lyapunov’s Function）

（1）Lyapunov 函数定义

设 $V(x)$ 是连续可微函数，定义其沿系统轨迹的导数：
$$
\dot{V}(x) = \frac{\partial V}{\partial x} f(x) = \nabla V(x)^\top f(x)
$$

若：

• $V(x) > 0, \ \forall x \ne 0$；
• $\dot{V}(x) \le 0, \ \forall x$；
  则系统稳定。

（2）解释步骤

1. 构造能量型函数 $V(x)$，例如 $V(x) = x^\top P x$；
2. 计算 $\dot{V}(x)$；
3. 若 $\dot{V}(x)$ 恒为负，则能量单调下降，系统收敛；
4. 若 $\dot{V}(x)$ 仅非正，则能量不增，系统不发散。

24.8 Lyapunov 定理（Lyapunov’s Theorem）

条件

设系统 $\dot{x} = f(x)$，且存在 $V(x)$ 满足：

1. $V(0) = 0, \ V(x) > 0, \forall x \ne 0$；
2. $\dot{V}(x) \le 0, \forall x$。

结论

• 若 $\dot{V}(x) \le 0$：系统稳定；
• 若 $\dot{V}(x) < 0$：系统渐近稳定；
• 若 $V(x)$ 在全空间径向无界且条件全局成立，则系统全局渐近稳定。

24.9 Lyapunov 函数术语表

条件	中文定义	英文名称
$V(0)=0, V(x)\ge0$	正半定	Positive semidefinite
$V(0)=0, V(x)>0$	正定	Positive definite
$\dot{V}(0)=0, \dot{V}(x)\le0$	负半定	Negative semidefinite
$\dot{V}(0)=0, \dot{V}(x)<0$	负定	Negative definite
$|x|\to\infty \Rightarrow V(x)\to\infty$	径向无界	Radially unbounded

24.10 Lyapunov 定理总结（总结性说明）

• 若存在连续可微的正定函数 $V(x)$，且其导数 $\dot{V}(x)$ 为负半定，则系统稳定；
• 若 $\dot{V}(x)$ 严格负定，则系统渐近稳定；
• 若 $V(x)$ 同时径向无界且定义于整个空间，则系统全局渐近稳定。

📘 最终总结

Lyapunov 方法的关键思想是通过“能量函数”的角度理解系统：

• $V(x)$ 表示系统的能量；
• $\dot{V}(x)$ 表示能量变化率；
• 若能量持续下降，则系统状态最终必定回到平衡点。

类型	条件	稳定性
$V>0$, $\dot{V}=0$	恒能系统	稳定（但可能不收敛）
$V>0$, $\dot{V}<0$	能量单调下降	渐近稳定
$V>0$, $\dot{V}<0$, 径向无界	全空间能量耗散	全局渐近稳定

Lyapunov 理论是一种“无需解方程即可判断系统稳定性”的方法，
是现代非线性控制与动力系统分析的基础工具。

25. 模型预测控制（Model Predictive Control, MPC）

25.1 引言（Introduction to Model Predictive Control）

模型预测控制（Model Predictive Control, MPC） 是一种先进的反馈控制策略，
其核心思想是在每个采样时刻利用系统的显式模型预测未来的系统行为，
并通过滚动优化（receding horizon）实时求解有限时域内的最优控制输入。

🧩 控制原理概述

在每个时刻 $ k $：

1. 测量当前状态：
   $$
   x_k
   $$

2. 求解有限时域最优控制问题：
   $$
   \min_{u_0, \dots, u_{N-1} }
   \sum_{j=0}^{N-1} \ell(x_j, u_j) + V_f(x_N)
   $$
   满足系统动力学约束与输入/状态约束：
   $$
   x_{j+1} = f(x_j, u_j), \quad (x_j, u_j) \in \mathcal{X} \times \mathcal{U}
   $$

3. 应用最优输入：
   $$
   u_k^* = u_0^*
   $$
   然后向前滚动预测窗口（receding horizon），重复上述步骤。

25.2 核心要素（Core Ingredients of Predictive Control）

• 显式内部模型（Explicit Internal Model）
  可以是线性（LTI）、线性时变（LTV）或非线性（Nonlinear）系统：
  $$
  x_{k+1} = f(x_k, u_k)
  $$

• 滚动时域思想（Receding Horizon Idea）
  控制器在每个采样周期重新预测与优化，始终基于最新状态进行反馈调整。

📘 注意：
MPC 并非单一算法，而是一个框架（framework），
不同的优化器、模型或代价函数定义会导致不同的 MPC 实现（线性、非线性、鲁棒等）。

25.3 为什么在机器人中使用 MPC（Why MPC for Robots）

在机器人控制中，MPC 的优势主要体现在同时处理约束（constraints）与多目标权衡（trade-offs）。

🧱 硬约束（Hard Constraints）

MPC 能够显式地将各种物理约束纳入优化问题：

• 执行器饱和（Actuator saturation）：
  $$
  \tau_{\min} \le \tau_k \le \tau_{\max}
  $$
• 关节、位置、速度、加速度限制（Joint/Position/Velocity/Acceleration limits）：
  $$
  q \in [q_{\min}, q_{\max}], \quad \dot{q} \in [\dot{q}_{\min}, \dot{q}_{\max}]
  $$
• 安全距离（Safety distances）：
  $$
  \text{dist}(x_k, \text{obstacles}) \ge d_{\text{safe} }
  $$

⚖️ 多目标代价函数（Multi-Objective Cost Function）

MPC 通过代价函数平衡精度（accuracy）、平滑性（smoothness）与能耗（energy）：

$$
J = \sum_{k=0}^{N-1}
|x_k - x_k^{\text{ref} }|_Q^2 +
|u_k|_R^2 +
|x_N - x_N^{\text{ref} }|_P^2
$$

其中：

• $ Q $：位置误差权重
• $ R $：控制输入权重
• $ P $：终端误差权重

🎯 参数调优与折中（Tuning and Trade-offs）

调节 $(Q, R, P)$ 可以在不同目标之间建立清晰的量化折中关系：

目标	增大权重	效果
精度（accuracy）	$ Q \uparrow $	跟踪误差减小，但控制更剧烈
平滑性（smoothness）	$ R \uparrow $	控制动作更平滑，但响应变慢
稳态误差（terminal accuracy）	$ P \uparrow $	最终状态更接近目标，代价更高

25.4 直观理解（Intuitive Understanding）

MPC 就像一个“预测型驾驶员”：

它不仅看到当前的路况，还能预判未来的转弯、坡度与障碍，
并提前调整油门与方向，使系统始终平稳且安全地运行。

25.5 一句话总结 🧠

MPC = 预测 + 优化 + 反馈。
它通过显式模型预测未来、求解最优输入，并实时滚动优化，
实现了传统控制无法兼顾的“约束处理 + 多目标最优”能力。

26. 线性化模型预测控制（Linearization and Linear MPC）

26.1 从连续到离散：采样与零阶保持（Sampling and Zero-Order Hold）

MPC 通常在**离散时间系统（Discrete-Time System）**上实现，
因此需要将连续时间模型离散化。

连续时间模型（Continuous LTI Model）

$$
\dot{x}(t) = A_c x(t) + B_c u(t)
$$

选择采样周期 $ T_s $，并对输入采用零阶保持（Zero-Order Hold, ZOH）：

$$
u(t) = u_k, \quad \text{for } t \in [kT_s, (k+1)T_s)
$$

在实际数字控制系统中，控制信号 $ u(t) $ 由计算机以离散时间生成，并在相邻采样周期内保持不变。这种**“采样-保持”机制称为零阶保持（ZOH）**

离散时间模型（Discrete-Time Model）

经过采样与保持，得到精确的离散化形式：

$$
x_{k+1} = A x_k + B u_k
$$

其中：

$$
A = e^{A_c T_s}, \quad
B = \int_0^{T_s} e^{A_c \tau} B_c , d\tau
$$

26.2 采样时间的选择（Choosing the Sampling Time $T_s$）

采样周期的选取至关重要——它决定了系统的预测精度与实时性之间的平衡。

🎯 目标

捕获系统最快的相关动态，同时保证优化问题（QP）规模适中。

“QP 规模”指的是该优化问题的变量数量和约束数量。换言之，它反映了每次求解时优化器需要处理的问题复杂度。

✅ 经验法则（Rule of Thumb）

$$
T_s \le 0.1 \tau_{\min}
$$

即在系统最小时间常数 $\tau_{\min}$ 上至少取 10 个采样点，
或者选择采样频率至少为闭环带宽的 10 倍。

⚙️ 常见频率范围（Typical Control Rates）

控制层级	典型频率范围
内环（力矩/速度环）	500 Hz – 2 kHz
外环（位置/轨迹跟踪）	50 Hz – 200 Hz

⚠️ 采样时间过大（Too Large $T_s$）

• 产生混叠（Aliasing）；
• 模型不匹配（Model mismatch）；
• 难以满足约束（Constraint violation）。

⚠️ 采样时间过小（Too Small $T_s$）

• 优化问题（QP）频繁求解，计算负载过高；
• 求解器可能错过实时截止期限（Solver misses deadlines）。

📘 总结：

选择合适的 $T_s$ 是 MPC 实时性与精度平衡的关键，
太慢会失真，太快会过载。

26.3 为什么要线性化（Why Linearization for MPC）

机器人动力学通常是非线性的：

$$
\dot{x} = f(x, u)
$$

然而，标准的线性 MPC（即二次规划 QP）仅适用于仿射系统（Affine Systems）：

$$
\dot{x} \approx A x + B u + c
$$

🧩 线性化方法（Linearization Approach）

• 在一个**平衡点（equilibrium）或标称轨迹（nominal trajectory）**附近展开；
• 使用泰勒展开的一阶近似构造线性模型；
• 在每次 MPC 滚动优化时，在线重线性化（re-linearization online）：
  $$
  \delta \dot{x} = A(t), \delta x + B(t), \delta u
  $$
  保证在当前状态附近的精确性（小偏差假设）。

📈 优势（Benefits）

• 转化为凸优化问题（convex QP）；
• 具有可预测的计算时间；
• 能直接处理约束条件；
• 适用于小范围调节与轨迹跟踪。

⚠️ 注意（Caveat）

仅在接近平衡点 $(x^*, u^*)$ 时有效。
若偏差过大，线性模型将失准，需重新线性化。

26.4 平衡点与轨迹线性化（Equilibria vs. Trajectories）

🧭 平衡点线性化（At an Equilibrium $(x^*, u^*)$）

$$
f(x^*, u^*) = 0
$$

则线性化系统为：

$$
\delta \dot{x} = A \delta x + B \delta u
$$

• 对应 线性时不变系统（LTI）；
• 适用于稳态调节与小扰动响应；
• 常用于姿态保持或位置维持。

🚗 轨迹线性化（At a Nominal Trajectory $(x^*(t), u^*(t))$）

• 系统沿时间变化的参考路径运动；
• 对应 线性时变系统（LTV）；
• MPC 使用参考输入 $u^*(t)$ 作为前馈项；
• 在每个时间步 $k$ 重新线性化：
  $$
  \delta x_{k+1} = A_k \delta x_k + B_k \delta u_k
  $$

📘 总结：

平衡点线性化用于稳定控制，
轨迹线性化用于动态跟踪。

26.5 线性与非线性 MPC 对比（Linear vs. Nonlinear MPC）

特性	线性 MPC	非线性 MPC (NMPC)
模型形式	$ x_{k+1} = A x_k + B u_k $	$ x_{k+1} = f(x_k, u_k) $
优化类型	二次规划（QP）	非线性规划（NLP）
可解性	快速、全局凸	精度高但非凸
计算复杂度	低	高
适用范围	局部线性区域	宽范围动态系统
主要挑战	模型局限	局部最优、实时性困难

📘 总结：

Linear MPC 在实时性与稳定性上具有优势，适合局部控制与工业机器人；
Nonlinear MPC 适合处理复杂动力学与高机动性任务，但计算代价更高。

27. 模型预测控制的标准形式（Standard Formulation of MPC）

27.1 基本概念（Fundamental Idea）

模型预测控制（Model Predictive Control, MPC）的核心是在有限预测时域（finite prediction horizon）内求解约束最优控制问题。
在每一个采样时刻，MPC 通过预测未来系统演化，优化未来一段时间内的输入序列，使系统状态尽可能接近期望轨迹或目标点。

MPC 的一般优化问题可以表示为：

$$
\min_{ {u_i}_{i=0}^{N-1} }
\sum_{i=0}^{N-1} \ell(x_i, u_i) + V_f(x_N)
$$

subject to:
$$
\begin{cases}
x_{i+1} = f(x_i, u_i), & i = 0, \dots, N-1, \
x_0 = \hat{x}_k, & \text{(当前测量状态)} \
g(x_i, u_i) \le 0, & \text{(一般不等式约束)} \
h(x_N) \le 0, & \text{(终端约束或稳定性条件)} \
u_i \in \mathcal{U},; x_i \in \mathcal{X}, & \text{(输入与状态约束)}
\end{cases}
$$

---

27.2 组成部分（Constituent Components）

该标准形式包含三个核心部分：

(1) 阶段代价函数（Stage Cost）

阶段代价函数定义为：

$$
\ell(x, u) = |x - x_{\text{ref} }|_Q^2 + |u|_R^2
$$

• 第一项衡量状态偏离目标 $x_{\text{ref} }$ 的程度；
• 第二项限制控制输入的大小，保证平滑性与能耗控制；
• 矩阵 $ Q $ 和 $ R $ 是正定加权矩阵，用于调节两者权重。

直观解释：

阶段代价是 MPC 的“即时损失”，它鼓励状态接近参考目标，同时惩罚剧烈的控制变化。

---

(2) 终端代价函数（Terminal Cost）

在预测时域的末尾，引入一个终端项来提升系统稳定性：

$$
V_f(x_N) = |x_N - x_{\text{ref} }|_P^2
$$

或与稳定终端集合 $ h(x_N) \le 0 $ 结合使用。

• $ P $：终端权重矩阵（通常由李雅普诺夫方程或黎卡提方程计算）。
• $ V_f $：保证状态在预测末尾收敛到稳定区域。

直观解释：

终端代价确保系统不会“提前停止优化”而偏离目标，
它为系统提供了“远视能力”，避免短期最优但长期失稳。

---

(3) 约束条件（Constraints）

MPC 的强大之处在于其显式处理约束：

1. 输入约束（Input Constraints）
   反映执行器物理极限：
   $$
   u_{\min} \le u_i \le u_{\max}
   $$

2. 状态约束（State Constraints）
   确保系统安全运行：
   $$
   x_{\min} \le x_i \le x_{\max}
   $$

3. 一般不等式约束（General Inequalities）
   表示复杂的几何或任务条件：
   $$
   g(x_i, u_i) \le 0
   $$

4. 终端约束（Terminal Constraints）
   保证最终状态位于可稳定控制的集合内：
   $$
   h(x_N) \le 0
   $$

---

27.3 预测模型与离散化（Prediction Model and Discretization）

MPC 依赖于一个能够预测系统未来状态的模型。
连续时间非线性动力学通常表示为：

$$
\dot{x} = f_c(x, u)
$$

通过选定采样周期 $T_s$，可将其离散化为：

$$
x_{k+1} \approx x_k + T_s f_c(x_k, u_k)
\quad \text{(Euler 离散化)}
$$

或采用更高精度的积分方法：

• RK2 / RK4（Runge–Kutta）：逐步积分精度更高；
• Collocation：在区间内部强制动力学一致；
• Multiple-shooting：将长时间预测分段优化以增强鲁棒性。

---

📘 不同离散化方法的特性比较

方法	特点	优点	缺点
Euler	一阶精度，简单快速	计算负担低	精度有限，误差积累
RK4	四阶精度	高精度稳定	计算量大
Collocation	约束连续性	高精度拟合	实现复杂
Multiple-shooting	分段优化	数值稳定性好	变量数量增加

---

27.4 优化问题结构（Optimization Problem Structure）

MPC 优化问题可总结为：

• 变量： 控制序列 ${u_0, \dots, u_{N-1}}$
• 目标： 最小化加权误差与控制能量；
• 约束： 动力学方程 + 安全限制 + 稳定条件。

当 $ f(x,u) $ 线性、$\ell(x,u)$ 二次时，
问题变为二次规划（Quadratic Program, QP）：

$$
\min_U \frac{1}{2} U^\top H U + F^\top U
\quad \text{s.t. } G U \le b
$$

这是线性 MPC 的常见形式，能保证全局最优与快速求解。

---

27.5 在机器人中的意义（Relevance to Robotics）

MPC 的标准形式特别适用于机器人系统，因为它：

• 自然适应约束性系统（例如关节极限、障碍物、安全距离）；
• 允许多目标调优（平衡精度、能耗、平滑度与安全性）；
• 支持非线性扩展（通过近似或直接求解 NMPC）。

在移动机器人、机械臂、无人机控制等领域，MPC 已成为最主流的约束最优控制框架。

---

27.6 一句话总结 🧠

标准 MPC 形式 = 预测模型 + 二次代价 + 约束条件。
它将“未来规划”转化为一个可实时求解的优化问题，
使机器人在动态环境中实现稳定、平滑且安全的自主控制。

28. 模型预测控制实例（Examples of Model Predictive Control）

在理解了模型预测控制（MPC）的标准形式与离散化原理之后，本节通过几个典型实例展示 MPC 如何应用于机器人系统，从线性移动机器人到非线性机械臂控制。

---

28.1 示例一：单轮差动机器人（Unicycle Robot）

🚗 连续时间运动学模型

单轮机器人（如移动底盘）具有如下连续时间模型：

$$
\dot{p}_x = v \cos \theta, \quad
\dot{p}_y = v \sin \theta, \quad
\dot{\theta} = \omega
$$

其中：

• $ (p_x, p_y) $：平面位置；
• $ \theta $：航向角；
• $ v, \omega $：线速度与角速度（控制输入）。

---

🔹 线性化（Linearization）

当机器人在近似直线运动（$\theta \approx 0, v \approx v_0$）时，可线性化：

$$
\dot{p}_x \approx v, \quad
\dot{p}_y \approx v_0 \theta, \quad
\dot{\theta} = \omega
$$

以矩阵形式表示为：

$$
\dot{x} = A_c x + B_c u
$$

其中：

$$
x =
\begin{bmatrix}
p_x \\ p_y \\ \theta
\end{bmatrix}, \quad
u = \begin{bmatrix}
v \\ \omega
\end{bmatrix}, \quad
A_c =\begin{bmatrix}
0 & 0 & 0 \\
0 & 0 & v_0 \\
0 & 0 & 0
\end{bmatrix}, \quad
B_c =\begin{bmatrix}
1 & 0 \\
0 & 0 \\
0 & 1
\end{bmatrix}
$$

---

🔸 离散化（Discrete-Time Form）

采用采样周期 $ T_s $ 并通过零阶保持（ZOH）离散化：

$$
A_d = e^{A_c T_s} \approx
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & T_s v_0 \\
0 & 0 & 1
\end{bmatrix}, \quad
B_d =
\begin{bmatrix}
T_s & 0 \\
0 & 0 \\
0 & T_s
\end{bmatrix}
$$

因此离散系统为：

$$
x_{k+1} = A_d x_k + B_d u_k
$$

---

⚙️ MPC 优化问题（QP Formulation）

预测时域长度 $N$ 下的优化问题：

$$
\min_{ {u_i} } \sum_{i=0}^{N-1} \big(|x_i - x_i^{\text{ref} }|_Q^2 + |u_i|_R^2\big) + |x_N - x_N^{\text{ref} }|_P^2
$$

subject to:
$$
x_{i+1} = A_d x_i + B_d u_i, \quad u_{\min} \le u_i \le u_{\max}, \quad x_{\min} \le x_i \le x_{\max}
$$

✅ 这是典型的线性 MPC（二次规划 QP）形式，
可用于路径跟踪、避障或稳定姿态等任务。

---

🧠 直观理解

MPC 通过预测机器人未来的运动轨迹，
在满足输入/状态约束的同时最小化轨迹偏差，
实现平滑、安全的路径跟踪控制。

---

28.2 示例二：两自由度机械臂（2-DOF Robot Arm）

🤖 动力学方程（Continuous Dynamics）

两自由度机械臂的动力学可由欧拉–拉格朗日方程给出：

$$
M(q)\ddot{q} + C(q, \dot{q})\dot{q} + g(q) = \tau
$$

其中：

• $q = [q_1, q_2]^\top$：关节角；
• $\dot{q}$：角速度；
• $\tau = [\tau_1, \tau_2]^\top$：关节力矩（控制输入）；
• $M, C, g$：分别为惯性矩阵、科氏项与重力项。

---

🔹 状态空间形式

定义状态 $x = [q, \dot{q}]^\top$，则：

$$
\dot{x} =
\begin{bmatrix}
\dot{q} \ M^{-1}(q)\big(\tau - C(q, \dot{q})\dot{q} - g(q)\big)
\end{bmatrix}
= f_c(x, u)
$$

---

🔸 离散化（RK4 Integration）

采用四阶 Runge–Kutta（RK4）离散化：

$$
x_{k+1} = x_k + \frac{T_s}{6}(k_1 + 2k_2 + 2k_3 + k_4)
$$

其中：
$$
\begin{aligned}
k_1 &= f_c(x_k, u_k), \
k_2 &= f_c(x_k + \tfrac{T_s}{2}k_1, u_k), \
k_3 &= f_c(x_k + \tfrac{T_s}{2}k_2, u_k), \
k_4 &= f_c(x_k + T_s k_3, u_k)
\end{aligned}
$$

RK4 具有高精度数值稳定性，适合 NMPC 使用。

---

⚙️ NMPC 优化问题（NLP Formulation）

$$
\min_{ {u_i} } \sum_{i=0}^{N-1} (|x_i - x_i^{\text{ref} }|_Q^2 + |u_i|_R^2) + |x_N - x_N^{\text{ref} }|_P^2
$$

subject to:
$$
x_{i+1} = \Phi_{\text{RK4} }(x_i, u_i; T_s), \quad \tau_{\min} \le u_i \le \tau_{\max}, \quad \dot{q}_{\min} \le \dot{q}_i \le \dot{q}_{\max}
$$

此时，优化问题为非线性规划（NLP），
通常需通过 SQP 或 interior-point 方法求解。

---

🧩 特点总结

对比项	线性 MPC	非线性 MPC
模型	线性近似 $x_{k+1}=A x_k + B u_k$	真正非线性 $x_{k+1}=f(x_k, u_k)$
优化类型	QP（二次规划）	NLP（非线性规划）
可解性	快速、凸	精确但计算代价高
应用场景	移动机器人、航迹跟踪	机械臂、无人机、复杂约束系统

---

28.3 示例三：带约束的温度控制系统（Thermal System MPC）

🌡️ 系统模型

考虑一维温度场（例如炉内温控或电子设备冷却）：

$$
\dot{T}(t) = -\alpha (T(t) - T_{\text{env} }) + \beta u(t)
$$

其中：

• $T(t)$：系统温度；
• $T_{\text{env} }$：环境温度；
• $u(t)$：加热功率（控制输入）；
• $\alpha, \beta > 0$：热传导系数与加热效率。

离散化形式：

$$
T_{k+1} = (1 - \alpha T_s)T_k + \beta T_s u_k
$$

---

⚙️ MPC 控制目标

• 目标温度 $T^{\text{ref} }$
• 输入限制 $0 \le u_k \le 1$
• 最小化能耗与温度误差：

$$
\min_{ {u_i} } \sum_{i=0}^{N-1} \big((T_i - T^{\text{ref} })^2 Q + u_i^2 R\big)
$$

该问题为一维 QP，可实时求解，用于空调系统、加热控制等场景。

---

28.4 总结（Summary）

示例	系统类型	离散化方式	优化类型	特点
单轮机器人	线性近似	ZOH / Euler	QP	快速求解，路径平滑
两自由度机械臂	非线性	RK4	NLP	高精度控制，复杂动态
温控系统	一维线性	Euler	QP	简单易实现，能耗最优

---

📘 一句话总结：

不论是差动机器人、机械臂还是温控系统，
MPC 的核心思想始终是——
“预测未来、最优控制、实时滚动”，
并通过模型离散化与优化算法实现动态环境下的智能决策。

29. 基于模型的动力学控制（Model-Based Dynamic Control）

29.1 引言（Introduction）

机器人系统的动力学通常具有显著的非线性特征，
例如惯性随构型变化、存在科氏力与离心力项、以及重力效应等。
在这种情况下，传统的线性控制（如 PD 控制）往往无法在全工作空间内保持稳定与高精度。

**基于模型的动力学控制（Model-Based Dynamic Control）**通过显式利用系统的动力学模型，
在控制律中对非线性项进行补偿或抵消，使得误差动力学接近线性系统。
这种方法不仅能提高跟踪精度，还能保证系统的可预测性与稳定性。

---

29.2 为什么需要基于模型的控制（Why Model-Based Control）

⚙️ 机器人动力学模型

多关节机器人系统的一般形式为：

$$
M(q)\ddot{q} + C(q, \dot{q})\dot{q} + g(q) = \tau
$$

其中：

• $M(q)$：惯性矩阵（与构型相关）；
• $C(q, \dot{q})$：科氏与离心项；
• $g(q)$：重力项；
• $\tau$：关节力矩（控制输入）。

这些非线性项导致系统难以直接使用线性控制器设计。
因此，基于模型的方法通过动力学补偿，使误差动态具有更好的可控性和可分析性。

---

🎯 核心目标

• 消除或补偿非线性效应；
• 获取“线性化”的误差动力学；
• 允许基于李雅普诺夫分析证明系统稳定性；
• 在不同负载或高动态任务下保持精确控制。

---

💡 优势总结

优势	描述
高精度跟踪	补偿动力学非线性后，误差趋于零
可预测瞬态	系统动态可被线性化处理，响应一致
稳定性可分析	可用能量函数或李雅普诺夫函数分析稳定性
适用场景广	高速轨迹、负载变化、力控任务等

---

29.3 符号定义（Notation and Error Representation）

误差定义

设参考轨迹为 $q_d(t)$，则定义：

$$
e = q - q_d, \quad \dot{e} = \dot{q} - \dot{q}_d
$$

即位置误差与速度误差。

参考轨迹光滑性

假设 $q_d(t)$、$\dot{q}_d(t)$、$\ddot{q}_d(t)$ 为二阶连续可导函数，且有界：

$$
|q_d(t)| \le M_0, \quad
|\dot{q}_d(t)| \le M_1, \quad
|\ddot{q}_d(t)| \le M_2, \quad \forall t
$$

输入与扰动

控制输入 $\tau \in \mathbb{R}^n$，外部扰动 $d \in \mathbb{R}^n$，
且扰动项有界，即 $|d(t)| \le D_{\max}$。

增益矩阵定义

$K_P, K_D, \Lambda, \Gamma, K, K_S$ 等均为对称正定矩阵（SPD），
它们决定系统的收敛速率与阻尼特性。

---

29.4 控制环结构（Model-Based Control Loop）

下图展示了典型的基于模型的控制闭环结构：

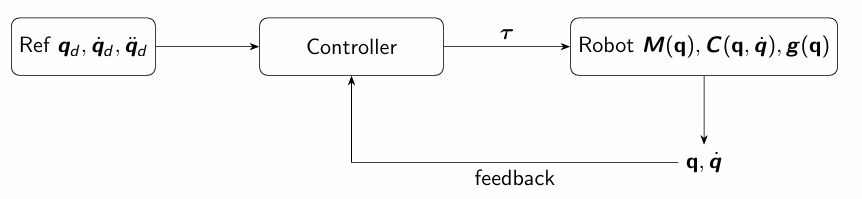
该控制回路表明控制器利用当前的状态反馈 $(q, \dot{q})$ 与参考轨迹 $(q_d, \dot{q}_d, \ddot{q}_d)$，
生成力矩指令 $\tau$，通过模型补偿项来消除非线性效应，使得系统整体表现如线性二阶系统。

---

29.5 应用场景（Use Cases）

1. 高精度轨迹跟踪（High-Precision Tracking）
   适用于高端工业机械臂（如协作机器人、焊接机器人），
   可在复杂路径中维持亚毫米级误差。

2. 高速运动控制（Fast Motion Control）
   在快速抓取、抛接、无人机姿态控制等任务中，
   通过动态补偿防止非线性惯性项引起的不稳定。

3. 负载变化补偿（Payload Variation Compensation）
   机器人在操作不同质量负载时，惯性矩阵 $M(q)$ 变化显著，
   基于模型控制可自动适应不同动态条件。

4. 仿人机器人控制（Humanoid and Bipedal Systems）
   用于保持平衡与协调动作，抵消重力与非线性相互作用。

---

29.6 一句话总结 🧠

基于模型的动力学控制通过利用系统模型补偿非线性项，
将复杂的机器人动力学转换为线性可控的误差系统，
从而实现高精度、高动态与高稳定性的控制性能。

30. 计算力矩控制（Computed Torque Control, CTC）

30.1 理论基础（From Inverse Dynamics Derivation）

计算力矩控制（CTC）是一种基于逆动力学补偿的非线性控制方法，
它利用系统模型将复杂的动力学方程“线性化”，从而将控制问题化简为多个独立的二阶子系统。

---

30.2 动力学模型（Robot Dynamics）

机器人系统的动力学方程为：

$$
M(q)\ddot{q} + C(q, \dot{q})\dot{q} + g(q) = \tau
$$

其中：

• $M(q)$：惯性矩阵；
• $C(q, \dot{q})$：科氏与离心项；
• $g(q)$：重力项；
• $\tau$：关节力矩输入。

---

30.3 控制目标（Goal）

希望系统的误差动态服从线性、可解耦的形式，例如：

$$
\ddot{e} + K_d \dot{e} + K_p e = 0
$$

其中：

• $e = q - q_d$：位置误差；
• $\dot{e} = \dot{q} - \dot{q}_d$：速度误差；
• $K_p \succ 0, K_d \succ 0$：正定增益矩阵。

---

30.4 控制律设计（Control Law Design）

为实现上述误差动态，设计一个辅助输入变量 $v$，并定义控制律：

$$
\tau = M(q) v + C(q, \dot{q})\dot{q} + g(q)
$$

其中辅助变量 $v$ 选为：

$$
v = \ddot{q}_d - K_d \dot{e} - K_p e
$$

将其代入系统动力学方程，得到闭环形式：

$$
M(q)\ddot{q} + C(q, \dot{q})\dot{q} + g(q)
= M(q)(\ddot{q}_d - K_d \dot{e} - K_p e) + C(q, \dot{q})\dot{q} + g(q)
$$

化简得：

$$
\ddot{e} + K_d \dot{e} + K_p e = 0
$$

---

30.5 闭环特性（Closed-Loop Behavior）

该闭环系统等价于解耦的二阶系统：

$$
\ddot{e}_i + k_{d,i} \dot{e}_i + k_{p,i} e_i = 0
$$

每个关节 $i$ 的动态都表现为一个二阶线性系统，
其自然频率与阻尼比由增益矩阵 $(K_p, K_d)$ 决定：

$$
\omega_n = \sqrt{K_p}, \quad \zeta = \frac{K_d}{2\sqrt{K_p}}
$$

因此，只需调整 $K_p$ 与 $K_d$，即可实现期望的动态响应与稳定性。

---

30.6 实际实现条件（Implementation Conditions）

为了实现精确的 CTC，需要以下条件：

1. 模型项可得：
   $M(q)$、$C(q, \dot{q})$、$g(q)$ 必须在每个控制周期计算或近似得到；
2. 参考轨迹已知且光滑：
   $q_d(t) \in C^2$，即已知 $\dot{q}_d$、$\ddot{q}_d$；
3. 可测状态：
   $q$ 通常可直接测量，$\dot{q}$ 可通过编码器差分或滤波估计；
4. 执行器可实现：
   电机或液压驱动器应能输出所需的扭矩指令（饱和单独处理）。

---

30.7 特点总结（Summary）

特性	说明
控制原理	基于逆动力学补偿
闭环结构	线性二阶系统
模型需求	高（需 $M,C,g$ 准确）
动态性能	优秀，响应快且精确
缺点	对建模误差与噪声敏感
改进方向	自适应控制、鲁棒控制、学习补偿等

---

30.8 直观理解（Intuitive View）

CTC 本质上是在每个控制周期精确反算系统动力学，
通过“前馈补偿 + 反馈校正”的方式让系统表现如理想线性系统：

$$
\text{Nonlinear system + Inverse model → Linear-like behavior}
$$

---

30.9 一句话总结 🧠

**计算力矩控制（CTC）**是利用动力学模型实现非线性系统线性化的核心方法，
它使每个关节的运动误差服从二阶线性系统，从而获得精确、可预测的轨迹跟踪性能。

31. 全状态反馈线性化（Full-State Feedback Linearization, Joint Space）

31.1 理念概述（Concept Overview）

**全状态反馈线性化（Full-State Feedback Linearization）是一种利用系统动力学模型实现精确输入输出解耦的控制方法。
通过在控制律中引入非线性补偿项，可以消除机器人动力学中的耦合效应与非线性项，使闭环系统表现为线性二阶系统。
这种方法是计算力矩控制（CTC）**的理论推广，也是非线性控制中的经典设计思路。

---

31.2 动力学模型（Robot Dynamics）

机器人系统的动力学方程为：

$$
M(q)\ddot{q} + C(q, \dot{q})\dot{q} + g(q) = \tau
$$

其中：

• $M(q)$：惯性矩阵；
• $C(q, \dot{q})$：科氏力与离心力矩阵；
• $g(q)$：重力项；
• $\tau$：关节力矩输入。

---

31.3 控制律（Inverse Dynamics Control Law）

设计基于逆动力学的控制律：

$$
\tau = M(q)(\ddot{q}_d - K_d \dot{e} - K_p e) + C(q, \dot{q})\dot{q} + g(q)
$$

其中：

• $e = q - q_d$；
• $\dot{e} = \dot{q} - \dot{q}_d$；
• $K_p, K_d$ 为对称正定矩阵。

通过将系统的非线性项 $C(q, \dot{q})\dot{q}$ 和 $g(q)$ 显式补偿，
系统误差方程变为线性形式。

---

31.4 闭环误差动力学（Closed-Loop Dynamics）

代入控制律后得到：

$$
\ddot{e} + K_d \dot{e} + K_p e = 0
$$

这是一个标准的二阶线性微分方程，
每个关节可视为独立的线性系统，
系统极点由矩阵 $K_p$ 与 $K_d$ 决定。

• 当 $K_d$ 较大时，系统响应更快但阻尼较强；
• 当 $K_p$ 较大时，稳态误差减小但超调可能增大。

---

31.5 理论解释（Interpretation）

• 输入状态线性化（Exact Input-State Linearization）：
  系统在关节空间被完全线性化，非线性耦合项被模型补偿掉；
• 解耦特性（Decoupling）：
  每个关节独立表现为二阶线性系统；
• 参数影响：
  系统的自然频率与阻尼比由 $(K_p, K_d)$ 共同设定。

---

31.6 李雅普诺夫稳定性分析（Lyapunov Stability Sketch）

定义候选李雅普诺夫函数：

$$
V = \frac{1}{2}\dot{e}^T M(q)\dot{e} + \frac{1}{2} e^T K_p e
$$

对其求导：

$$
\dot{V} = -\dot{e}^T K_d \dot{e} \le 0
$$

因此系统渐近稳定，
且误差 $e(t)$ 与 $\dot{e}(t)$ 均随时间趋于零。

---

31.7 实际意义（Practical Implications）

• 精确建模是关键，否则补偿误差会引入动态不稳定；
• 在高精度控制与轨迹跟踪中，全状态反馈线性化能显著提升性能；
• 常用于：
  • 高速机械臂；
  • 双足机器人姿态稳定；
  • 飞行器姿态与轨迹控制。

---

32. 输入输出线性化（Input–Output Linearization, Task Space）

32.1 引言（Motivation）

在许多任务中，我们并不直接控制关节变量 $q$，
而是希望控制**任务空间（Task Space）**中的输出变量，例如：

$$
y = h(q) \in \mathbb{R}^m
$$

其中 $h(q)$ 是从关节空间到任务空间的光滑映射函数。

例如：

• 末端执行器的位置 $(x, y, z)$；
• 姿态角 $(\phi, \theta, \psi)$；
• 或者其他与任务相关的函数（如抓取力、传感器视角等）。

---

32.2 任务空间动力学（Task Space Dynamics）

从关节动力学：

$$
M(q)\ddot{q} + C(q, \dot{q})\dot{q} + g(q) = \tau
$$

映射到任务空间变量 $y = h(q)$，
其一阶、二阶导数为：

$$
\dot{y} = J(q)\dot{q}, \quad \ddot{y} = J(q)\ddot{q} + \dot{J}(q, \dot{q})\dot{q}
$$

其中 $J(q) = \frac{\partial h}{\partial q}$ 为雅可比矩阵。

---

32.3 控制目标与设计（Goal and Control Law）

目标：使任务空间误差 $e_y = y - y_d$ 满足线性闭环动态：

$$
\ddot{e}_y + K_{dy}\dot{e}_y + K_{py} e_y = 0
$$

设计控制律：

$$
\tau = M(q)J(q)^{-1} \left( \ddot{y}_d - K_{dy}\dot{e}_y - K_{py} e_y - \dot{J}(q, \dot{q})\dot{q} \right) + C(q, \dot{q})\dot{q} + g(q)
$$

当 $J(q)$ 非奇异时，该控制律实现任务空间的精确线性化。

---

32.4 实际意义与对比（Comparison with Joint-Space）

控制方式	控制变量	优点	缺点
关节空间线性化	$q$	结构简单，稳定性易分析	不直接控制末端位置
任务空间线性化	$y = h(q)$	直观控制末端轨迹	依赖 $J(q)$ 及其导数，奇异点敏感

---

32.5 结论（Summary）

全状态反馈线性化与输入输出线性化是非线性控制中最核心的两种补偿策略。
前者在关节空间实现完全线性化，后者在任务空间直接控制末端运动。
它们共同构成了基于模型控制（Model-Based Control）的理论基础，
在高精度机器人控制、航空航天系统、仿人运动控制等领域具有广泛应用。

33. 相对阶与反馈线性化控制律（Relative Degree and Control Law）

33.1 从关节动力学出发（From Joint Dynamics）

机器人任务空间动力学可由关节空间动力学导出：

$$
\ddot{y} = J(q)M(q)^{-1}\big(\tau - C(q, \dot{q})\dot{q} - g(q)\big) + \dot{J}(q, \dot{q})\dot{q}
$$

其中：

• $y = h(q)$ 为任务空间输出；
• $J(q)$ 为雅可比矩阵；
• $M(q)$、$C(q, \dot{q})$、$g(q)$ 分别为惯性矩阵、科氏/离心项与重力补偿项；
• $\tau$ 为控制输入（关节力矩）。

---

33.2 观察（Observation）

控制输入 $\tau$ 直接出现在输出的二阶导数 $\ddot{y}$ 中，
因此该系统的相对阶（Relative Degree）为 2。

这意味着：

• 系统从输入 $\tau$ 到输出 $y$ 之间存在两个积分环节；
• 控制目标应在加速度层面（$\ddot{y}$）进行补偿与线性化。

---

33.3 辅助输入的定义（Auxiliary Input Design）

为线性化系统输出动态，引入辅助输入 $v$，并定义控制律：

$$
\tau = M(q)J(q)^{\top} \Big[ v - \dot{J}(q, \dot{q})\dot{q} + J(q)M(q)^{-1}\big(C(q, \dot{q})\dot{q} + g(q)\big) \Big]
$$

代入后得：

$$
\ddot{y} = v
$$

结果是：非线性机器人动力学被完全抵消，输入输出映射成为线性形式。

---

33.4 控制律直观意义（Interpretation）

该控制律的核心思想是通过对系统动力学的精确建模与补偿，
将复杂的非线性动力学方程转化为任务空间内的线性二阶系统。

在此情况下，$v$ 成为一个“虚拟控制输入”，可以用经典线性控制理论设计。

---

34. 误差动态与控制设计（Error Dynamics and Comparison）

34.1 误差定义（Define Errors）

任务空间误差定义为：

$$
e = y - y_d, \quad \dot{e} = \dot{y} - \dot{y}_d
$$

选择辅助输入为：

$$
v = \ddot{y}_d - K_d \dot{e} - K_p e
$$

代入线性化系统 $\ddot{y} = v$，得到闭环误差动态：

$$
\ddot{e} + K_d \dot{e} + K_p e = 0
$$

该闭环方程与前面关节空间的线性化系统完全一致，
说明反馈线性化在任务空间与**计算力矩控制（CTC）**在关节空间具有等价关系。

---

34.2 比较（Comparison）

控制策略	控制变量	数学形式	特点
CTC（Computed Torque Control）	关节空间 $q$	$\ddot{e} + K_d \dot{e} + K_p e = 0$	精确控制每个关节；结构简单
反馈线性化（Feedback Linearization）	任务空间 $y$	$\ddot{e}_y + K_{dy}\dot{e}_y + K_{py}e_y = 0$	直接控制末端执行器的运动轨迹

✅ CTC 是反馈线性化的一种特例（在关节空间下实现）。

---

35. 优势与挑战（Advantages and Challenges）

35.1 优势（Advantages）

• ✅ 输入–输出线性化精确：
  使任务变量（如末端位置）与输入力矩之间的动态完全线性。
• ✅ 直接控制任务变量：
  适合末端轨迹控制、力控、交互控制等任务。
• ✅ 便于设计线性控制器：
  线性化后可直接使用 PD、LQR 等线性控制理论进行设计。

---

35.2 挑战（Challenges）

挑战	说明
对模型精度要求高	需要完整的 $M(q)$、$C(q, \dot{q})$、$g(q)$、$J(q)$ 信息
对参数误差敏感	建模误差或摩擦未建模项会导致非线性补偿失效
执行器饱和问题	力矩上限会破坏线性化效果，需额外饱和处理

---

35.3 实践应用（Practical Applications）

• 机械臂末端轨迹控制（如抓取、装配、焊接）；
• 医疗机器人和康复机器人（高精度运动控制）；
• 飞行与水下机器人姿态线性化控制；
• 人形机器人行走与稳定控制。

---

35.4 一句话总结 🧩

**反馈线性化（Feedback Linearization）**通过对非线性动力学的精确补偿，
将复杂的机器人系统转化为线性二阶动态结构，
使得任务空间的轨迹跟踪可以像控制线性系统一样简单明了。

36. 自适应控制（Adaptive Control）

36.1 动机（Motivation）

• 真实系统存在不确定性：
  参数（质量、摩擦、阻力、空气动力等）通常无法被精确获取。

• 问题：
  若使用固定控制器且参数设定错误，系统可能失去稳定性或出现跟踪误差。

• 自适应思想（Adaptive Idea）：

  • 在线估计未知参数；
  • 根据误差信号实时调整控制器参数。

• 主要收益（Benefit）：
  控制器具备“自我调整能力”，能在存在不确定性的情况下保持稳定与精确跟踪。

---

36.2 一般形式（General Form）

对于一般非线性系统：

$$
\dot{x} = f(x, u), \quad y = h(x)
$$

自适应假设：
系统的动力学在未知参数上是线性依赖的：

$$
f(x, u) = Y(x, u)\theta
$$

其中：

• $Y(x, u)$：已知的回归矩阵（regressor），由可测信号构成；
• $\theta$：未知但常数的参数向量。

控制目标：
设计控制律 $u(x, \hat{\theta})$ 及参数更新律 $\dot{\hat{\theta}}$，
使得即便 $\theta$ 未知，也能保证输出 $y(t) \to y_d(t)$。

---

36.3 自适应控制回路（Adaptive Control Loop）

控制结构通常包括：

1. 内环（Inner Loop）：控制器，根据当前参数估计计算控制输入 $\tau$；
2. 外环（Outer Loop）：自适应律（Adaptation Law），根据误差信号调整参数 $\hat{\theta}$；
3. 参考模型（Reference Model）：提供理想响应 $y_m$；
4. 误差信号（$e = y - y_m$）：用于调整参数与控制律。

该结构保证控制器能动态适应模型不确定性。

---

36.4 机器人系统中的自适应控制（Adaptive Control for Robotics）

机器人动力学模型为：

$$
M(q)\ddot{q} + C(q, \dot{q})\dot{q} + g(q) = \tau
$$

满足标准性质：

• $M(q) = M(q)^{\top} \succ 0$（对称正定）；

• $\dot{M}(q, \dot{q}) - 2C(q, \dot{q})$ 为反对称矩阵；

• 线性参数化（Linear Parameterization）：

  对任意 $(\xi, \zeta)$：

  $$
  M(q)\xi + C(q, \dot{q})\zeta + g(q)
  = Y(q, \dot{q}, \zeta, \xi)\theta
  $$

其中：

• $Y(\cdot)$ 是已知的回归矩阵；
• $\theta$ 是未知但常数的系统参数向量。

通过该形式，可以将动力学不确定性转化为参数估计问题，
结合自适应律实现实时补偿。

37. 自适应 Slotine–Li 控制（Adaptive Slotine–Li Control）

37.1 跟踪设定与滤波误差（Tracking Setup & Filtered Error）

设定期望轨迹 $q_d(t)$，该轨迹为二阶可导且有界。
定义跟踪误差与滤波（滑模）误差为：

$$
e := q - q_d, \quad s := \dot{e} + \Lambda e
$$

其中 $\Lambda = \Lambda^{\top} > 0$ 为设计矩阵。
再定义参考速度与加速度：

$$
\dot{q}_r := \dot{q}_d - \Lambda e, \quad
\ddot{q}_r := \ddot{q}_d - \Lambda \dot{e}
$$

于是可得：

$$
s = \dot{q} - \dot{q}_r, \quad
\dot{s} = \ddot{q} - \ddot{q}_r
$$

滤波误差 $s$ 表示系统当前速度与期望参考速度的偏差，是控制器的核心反馈变量。

---

37.2 回归模型与控制律（Regressor, Control Law, and Adaptation）

基于机器人动力学的线性参数化性质：

$$
M(q)\ddot{q}_r + C(q, \dot{q})\dot{q}_r + g(q)
= Y(q, \dot{q}, \dot{q}_r, \ddot{q}_r)\theta
$$

Slotine–Li 自适应控制律定义为：

$$
\tau = Y(q, \dot{q}, \dot{q}_r, \ddot{q}_r)\hat{\theta} - K_d s
$$

其中：

• $K_d = K_d^{\top} > 0$：反馈增益矩阵；
• $\hat{\theta}$：参数估计值；
• $Y(\cdot)$：已知的回归矩阵。

参数更新律（Adaptation Law）：

$$
\dot{\hat{\theta}} = -\Gamma Y(q, \dot{q}, \dot{q}_r, \ddot{q}_r)^{\top}s
$$

其中 $\Gamma = \Gamma^{\top} > 0$ 为自适应增益矩阵。

控制律补偿了系统的动力学项，而参数更新律根据实时误差信号调整模型估计值。

项	数学形式	功能	直觉类比
$Y(q, \dot{q}, \dot{q}_r, \ddot{q}_r)\hat{\theta}$	前馈项	抵消非线性与耦合项	“预见性补偿”
$-K_d s$	反馈项	抑制误差与振荡	“阻尼校正”
$\dot{\hat{\theta}} = -\Gamma Y^{\top}s$	自适应律	实时调整参数估计	“学习与自校正”

---

37.3 闭环误差动力学（Closed-Loop Error Dynamics）

将控制律代入系统方程：

$$
M(q)\dot{s} + C(q, \dot{q})s + K_d s
= Y(q, \dot{q}, \dot{q}_r, \ddot{q}_r)\tilde{\theta}
$$

其中 $\tilde{\theta} = \hat{\theta} - \theta$ 为参数估计误差。

---

37.4 李雅普诺夫稳定性分析（Lyapunov Stability Analysis）

定义李雅普诺夫候选函数：

$$
V = \frac{1}{2}s^{\top}M(q)s + \frac{1}{2}\tilde{\theta}^{\top}\Gamma^{-1}\tilde{\theta}
$$

求导：

$$
\dot{V} = s^{\top}(C s + M\dot{s}) + \tilde{\theta}^{\top}\Gamma^{-1}\dot{\tilde{\theta}}
$$

利用动力学矩阵的反对称性质与自适应律可得：

$$
\dot{V} = -s^{\top}K_d s \le 0
$$

表明系统能量单调下降，因此闭环系统稳定。

---

37.5 稳定性结论（Stability Conclusions）

根据 $\dot{V} = -s^{\top}K_d s$，可得：

• $V(t)$ 单调不增且下界有界 $\Rightarrow s(t), \tilde{\theta}(t)$ 有界；
• $s^{\top}K_d s \in L_2 \cap L_{\infty}$；
• $q, \dot{q}, \dot{q}_r$ 有界 $\Rightarrow \dot{s}$ 有界；
• 由 Barbalat 引理：$s(t) \to 0$；
• 因为 $s = \dot{e} + \Lambda e \to 0$，所以 $e(t) \to 0$ 指数收敛。

---

37.6 结果总结（Result）

结论：

• 关节跟踪误差 $e(t)$ 全局收敛到 0；
• 参数 $\theta$ 即使未知，控制器仍可保证稳定与精确跟踪；
• Slotine–Li 控制是自适应控制与动力学补偿的完美结合，
  兼顾实时性、稳定性与鲁棒性。

38. 滑模控制（Sliding Mode Control, SMC）

38.1 动机与核心思想（Motivation & Core Idea）

• 目标：在存在匹配扰动 $d(t)$（通过输入通道作用）和模型不确定性的情况下，实现对期望轨迹 $q_d(t)$ 的鲁棒跟踪。
• SMC 思路：设计滑模面 $s(q,\dot{q},t)=0$ 并构造控制，使轨迹在有限时间内到达该面（reaching phase），并在该面上按期望动力学滑行（sliding phase），从而获得对匹配扰动的强鲁棒性。

---

38.2 机器人模型与关键性质（Robot Model & Key Property）

连续关节空间动力学带扰动：

$$
M(q)\ddot{q} + C(q,\dot{q})\dot{q} + g(q) = \tau + d(t)
$$

重要性质（用于分析）：

• $M(q)=M(q)^\top \succ 0$；
• $\dot{M}(q,\dot{q}) - 2C(q,\dot{q})$ 为反对称矩阵（skew-symmetric）；
• 假设扰动分量有界： $|d_i(t)| \le \Delta_i$（对每个关节分量）。

---

38.3 跟踪误差与滑模变量（Tracking Errors & Sliding Variable）

定义：
$$
e := q - q_d, \qquad \dot{e} := \dot{q} - \dot{q}_d
$$

滑模（滤波）误差：
$$
s := \dot{e} + \Lambda e, \qquad \Lambda = \Lambda^\top \succ 0
$$

在 $s=0$ 上，误差满足 $\dot{e} + \Lambda e = 0 \Rightarrow e(t)=e(0)e^{-\Lambda t}\to 0$，因此到达并保持在 $s=0$ 即实现期望误差衰减。

---

38.4 推导 $\dot{s}$ 与关键平衡（Deriving $\dot{s}$）

从动力学：
$$
\ddot{q} = M(q)^{-1}\big(\tau - C(q,\dot{q})\dot{q} - g(q) + d(t)\big)
$$

参考速度/加速度定义（与前节一致）：
$$
\dot{q}_r := \dot{q}_d - \Lambda e,\qquad \ddot{q}_r := \ddot{q}_d - \Lambda \dot{e}
$$

有 $s = \dot{q} - \dot{q}_r$ 与 $\dot{s} = \ddot{q} - \ddot{q}_r$。乘以 $M$ 并加减 $C\dot{q}_r$ 得：

$$
M\dot{s} + C s = \tau - \underbrace{\big(M\ddot{q}_r + C\dot{q}_r + g\big)}_{\tau_{eq}} + d(t)
$$

即关键平衡为：
$$
M\dot{s} + C s = (\tau - \tau_{eq}) + d(t).
$$

---

38.5 到达律与李雅普诺夫分析（Reaching Law）

取李雅普诺夫函数：
$$
V_s = \tfrac{1}{2} s^\top M(q) s.
$$

因反对称性可得：
$$
\dot{V}_s = s^\top (M\dot{s} + C s) = s^\top\big((\tau - \tau_{eq}) + d\big).
$$

为了保证有限时间到达滑模面，应设计 $u := \tau - \tau_{eq}$ 使得
$$
\dot{V}_s \le -\alpha |s|_1, \quad \alpha>0.
$$

若成立，则 $s(t)$ 在有限时间到达 0（componentwise arguments 给出线性衰减界）。

---

38.6 经典 SMC 控制律与鲁棒条件（Classic SMC & Robustness）

取不连续切换控制（理想分析）：
$$
u = -K,\operatorname{sgn}(s), \qquad K=\operatorname{diag}{k_i}\succ 0,
$$
即 $\tau = \tau_{eq} + u$。

代入 $\dot{V}_s$ 给出：
$$
\dot{V}_s = s^\top(-K\operatorname{sgn}(s) + d) = -\sum_i k_i|s_i| + \sum_i d_i s_i.
$$

若 $|d_i s_i| \le \Delta_i |s_i|$，则
$$
\dot{V}_s \le -\sum_i (k_i - \Delta_i)|s_i|.
$$

设计规则： 选取 $k_i > \Delta_i$，则 $\dot{V}_s \le -\alpha|s|_1$，保证有限时到达性与鲁棒性。

---

38.7 抖振（Chattering）与边界层（Boundary Layer）

• 理想 $\operatorname{sgn}(s)$ 导致高频切换（chattering）；执行器和传感器无法无限快切换 -> 实际系统出现小幅高频振荡，带来振动和磨损。
• 常用缓和方法：边界层饱和函数
  $$
  u = -K,\operatorname{sat}(s/\phi),\qquad
  \operatorname{sat}(z)=\begin{cases}
  \operatorname{sgn}(z), & |z|\ge 1,\[4pt]
  z, & |z|<1,
  \end{cases}
  $$
  这里取 $\operatorname{sat}(s/\phi)$ 表示分量式的饱和（bandwidth $\phi$）。
• 边界层去除抖振，但引入终值误差（ultimate bound）。边界层规模与稳态误差成正比。

---

38.8 完整关节空间 SMC（Complete SMC Law）

将名义等效力矩与切换项合并：

$$
\tau_{eq} = M(q)(\ddot{q}_d - \Lambda \dot{e}) + C(q,\dot{q})\dot{q} + g(q)
$$

$$
\tau = \tau_{eq} - K,\operatorname{sat}(s/\phi)
$$

闭环在 $s$ 上满足：
$$
M\dot{s} + C s = -K,\operatorname{sat}(s/\phi) + d,
$$
从而可证明到达性与最终有界性（ultimate boundedness）。

---

38.9 二阶滑模（Super-Twisting）以减小抖振（Reduced Chattering）

为获得连续控制且降低抖振，可采用 super-twisting（二阶 SMC）形式（每个关节 $i$）：

$$
u_i = -k_{1i} |s_i|^{1/2}\operatorname{sgn}(s_i) + v_i,\qquad
\dot{v}i = -k{2i}\operatorname{sgn}(s_i),
$$

再将 $u$ 注入為 $\tau = \tau_{eq} + u$。该方法给出连续（累积）控制输入，能显著抑制抖振，并在满足扰动导数有界及增益条件下实现有限时收敛。

---

38.10 要点回顾（Takeaways）

• 设计 $s=\dot{e}+\Lambda e$ 编码期望误差衰减。
• 用 $\tau_{eq}$ 抵消名义动力学，用 $-K,\operatorname{sat}(s/\phi)$ 提供鲁棒性并抑制抖振。
• 用 $V_s=\tfrac{1}{2}s^\top M s$ 证明可达性；选择 $k_i>\Delta_i$。
• 边界层 $\phi$ 给出终值界： $|s_i| \le (\phi_i \Delta_i)/k_i$。
• 在执行器和传感器现实约束下调参 $(\Lambda,K,\phi)$；如需更少抖振可考虑 super-twisting。

---

39. 四类情形中 $\tau$ 的作用

39.1 (A) 关节空间逆动力学 / 计算力矩控制（CTC, Joint space）

控制律：
$$
\tau = M(q),v + C(q,\dot{q})\dot{q} + g(q),\qquad v = \ddot{q}_d - K_d\dot{e} - K_p e
$$

$\tau$ 的作用与直觉：

• 前馈 / 等效部分 $M v + C\dot{q} + g$ 精确抵消名义动力学，使闭环误差动力学成为线性二阶： $ \ddot{e} + K_d\dot{e} + K_p e = 0$（在模型准确时）。
• 完全依赖精确模型；不含自适应或切换项；优点是高跟踪精度且无抖振；缺点对建模误差或快速扰动敏感。

---

39.2 (B) 任务空间输入—输出线性化（CTC, Task-space）

任务空间力与映射：
$$
F_{eq} = \Lambda(\ddot{x}_d - \Lambda_x \dot{e}_x) + \bar{\Xi}\dot{x} + p,\qquad F = F_{eq} - K_x\operatorname{sat}(s_x/\phi_x)
$$
关节力矩由雅可比映射：
$$
\tau = J(q)^\top F
$$

$\tau$ 的作用与直觉：

• 先在任务空间构造所需的力 $F$（等效前馈 + 鲁棒切换/饱和项），再通过 $\tau = J^\top F$ 把這些力映射回关节力矩。
• 优点是直接控制末端/任务变量（位置、力等）；仍需名义的模型/雅可比；若用饱和/边界层可减小抖振。

---

39.3 (C) Slotine–Li 自适应

控制律：
$$
\tau = Y(q,\dot{q},\dot{q}_r,\ddot{q}_r),\hat{\theta} - K_d s
$$
自适应律：
$$
\dot{\hat{\theta}} = -\Gamma Y^\top s
$$

$\tau$ 的作用与直觉：

• 前馈项 $Y\hat{\theta}$ 用在线估计的参数替代精确 $M\ddot{q}_r + C\dot{q}_r + g$，实现对名义动力学的补偿（当 $\hat{\theta}\approx\theta$ 时效果很好）。
• 反馈项 $-K_d s$ 提供阻尼與修正以对抗估计误差與瞬时扰动。
• 优点：在参数未知但固定（或慢变）时能保证渐近收敛且无抖振；缺点：对快变扰动/未建模动态的瞬时鲁棒性不及 SMC。

---

39.4 (D) 滑模控制（SMC）

名义等效项：
$$
\tau_{eq} = M(q)(\ddot{q}_d - \Lambda \dot{e}) + C(q,\dot{q})\dot{q} + g(q)
$$
切换 / 鲁棒项（示例，带边界层）：
$$
\tau = \tau_{eq} - K,\operatorname{sat}(s/\phi)
$$
（理想形式可用 $-K\operatorname{sgn}(s)$）

$\tau$ 的作用與直觉：

• $\tau_{eq}$ 抵消名义动力学，讓系統“就绪”做到滑模；額外項 $-K\operatorname{sat}(\cdot)$ 提供能量注入/抽取以克服匹配扰动，强制 $s$ 在有限时间到达 0。
• 优点：对有界匹配扰动有强鲁棒性与有限时收敛；缺点：理想切换会导致抖振，需用边界层或二阶 SMC（super-twisting）抑制。

---

39.5 简要比较（Compact Comparison）

面向	前馈（名义）	额外项	需求	鲁棒/抖振
CTC	精确 $M v + C\dot{q}+g$	无	精确模型	精度高；对扰动敏感
Task-space	$F_{eq}$ 映射 $J^\top F_{eq}$	$-K_x\operatorname{sat}$	$J,\Lambda$ 等	控制末端直观；受雅可比奇异影响
Slotine–Li	$Y\hat{\theta}$（估计）	$-K_d s$	线性参数化 $Y\theta$	无抖振；对快变扰动弱
SMC	$\tau_{eq}$	$-K\operatorname{sgn/sat}$	扰动上界 $\Delta$	有限时鲁棒；需防抖振

Approach	Nominal Feedforward	Additional Term	Requirements	Robustness / Chattering
CTC, joint space	Exact $M v + C\dot{q} + g$	None	Accurate model	High precision; sensitive to disturbances
CTC task-space	$F_{eq}$ mapped via $J^\top F_{eq}$	$-K_x \operatorname{sat}$	Requires $J$, $\Lambda$, etc.	Intuitive end-effector control; affected by Jacobian singularities
Slotine–Li	$Y\hat{\theta}$ (estimated)	$-K_d s$	Linear parameterization $Y\theta$	No chattering; weaker against fast-varying disturbances
SMC	$\tau_{eq}$	$-K,\operatorname{sgn/sat}$	Requires disturbance bound $\Delta$	Finite-time robustness; potential chattering (needs suppression)

---

39.6 设计建议（Practical Guidance）

• 若模型可信、需求最高精度：优先 CTC。
• 若关心末端任务（位置/力）且希望用同样的鲁棒手段：用 Task-space 控制（$F$ 然后 $\tau=J^\top F$）。
• 若参数未知但较慢变化且希望无抖振：Slotine–Li。
• 若扰动大且需有限时鲁棒性：SMC（并用边界层或 super-twisting 控制抖振）。
• 实务上常把名义补偿 $\tau_{eq}$ 与自适应或滑模项结合，以兼顾精度與鲁棒性。

---

一句话总结： 四类方法都包含“名义补偿/前馈”部分（抵消 $M,C,g$ 或其估计），但附加项不同：CTC 直接线性化、Task-space 先在任务空间设计力再映射、Slotine–Li 用在线估计替代精确模型并加线性反馈、SMC 则在名义补偿上再加切换/鲁棒项以实现有限时鲁棒性。

---

🍀后记🍀
博客的关键词集中在编程、算法、机器人、人工智能、数学等等，持续高质量输出中。
🌸唠嗑QQ群：兔叽の魔术工房 (942848525)
⭐B站账号：白拾ShiroX（活跃于知识区和动画区）
✨GitHub主页：yhbcode000（工程文件）
⛳Discord社区：AierLab（人工智能社区）