:star2:基本绘图
:star:绘图核心API
案例: 绘制简单直线
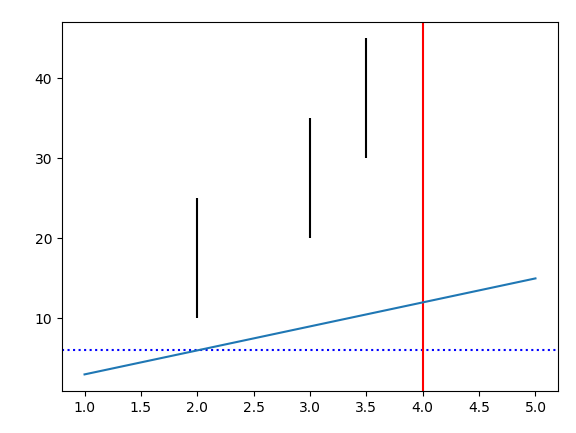
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| import numpy as np
import matplotlib.pyplot as plt
x = np.array([1, 2, 3, 4, 5])
y = np.array([3, 6, 9, 12, 15])
plt.axhline(y=6, ls=":", c="blue")
plt.axvline(x=4, ls="-", c="red")
plt.vlines([2, 3, 3.5],
[10, 20, 30],
[25, 35, 45])
[],[],[] 位置,开始位置,结束位置
plt.plot(x, y) ************************************
plt.show()
|
:star:设置线型、线宽
linestyle: 设置线型,常见取值有实线(‘-’)、虚线(‘–’)、点虚线(‘-.’)、点线(‘:’)
linewidth:线宽
color:颜色(red, blue, green)
英文单词: red blue green black oragered
字符串: #aabbcc
元组: (0.3,0.4,0.5) r,g,b
(0.3,0.4,0.5,0.6) r,g,b,a
alpha: 设置透明度(0~1之间)
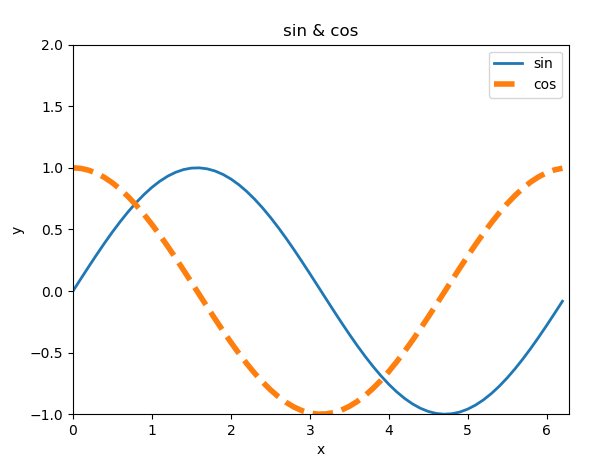
案例:绘制正弦、余弦曲线,并设置线型、线宽、颜色、透明度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
import numpy as np
import matplotlib.pyplot as plt
import math
x = np.arange(0, 2 * np.pi, 0.1)
print(x)
y1 = np.sin(x)
y2 = np.cos(x)
plt.plot(x, y1, label="sin", linewidth=2)
plt.plot(x, y2, label="cos", linestyle="--", linewidth=4)
plt.xlabel("x")
plt.ylabel("y")
plt.xlim(0, 2 * math.pi)
plt.ylim(-1, 2)
plt.title("sin & cos")
plt.legend()
plt.show()
|
:star:设置坐标轴范围
语法:
1
2
3
4
5
6
|
plt.xlim(x_limt_min, x_limit_max)
plt.ylim(y_limt_min, y_limit_max)
|
:star:设置坐标刻度
语法:
1
2
3
4
5
6
|
plt.xticks(x_val_list , x_text_list )
plt.yticks(y_val_list , y_text_list )
|
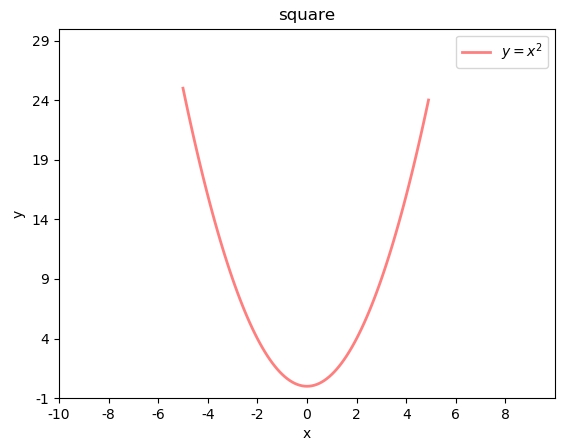
案例:绘制二次函数曲线
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
import numpy as np
import matplotlib.pyplot as plt
import math
x = np.arange(-5, 5, 0.1)
print(x)
y = x ** 2
plt.plot(x, y, label="$y = x ^ 2$",
linewidth=2,
color="red",
alpha=0.5)
plt.xlabel("x")
plt.ylabel("y")
plt.xlim(-10, 10)
plt.ylim(-1, 30)
x_tck = np.arange(-10, 10, 2)
x_txt = x_tck.astype("U")
plt.xticks(x_tck, x_txt)
y_tck = np.arange(-1, 30, 5)
y_txt = y_tck.astype("U")
plt.yticks(y_tck, y_txt)
plt.title("square")
plt.legend(loc="upper right")
plt.show()
|
刻度文本的特殊语法 – LaTex排版语法字符串
1
2
3
4
| r'$x^n+y^n=z^n$', r'$\int\frac{1}{x} dx = \ln |x| + C$', r'$-\frac{\pi}{2}$'
r'$latex表达式$'
|
$$
x^n+y^n=z^n, \int\frac{1}{x} dx = \ln |x| + C, -\frac{\pi}{2}
$$
:star:设置坐标轴
坐标轴名:left / right / bottom / top
1
2
3
4
5
6
7
8
9
10
11
|
ax = plt.gca()
axis = ax.spines['坐标轴名']
axis.set_position(('data', val))
axis.set_color(color)
|
案例:设置坐标轴格式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
import matplotlib.pyplot as plt
ax = plt.gca()
axis_b = ax.spines['bottom']
axis_b.set_position(('data', 0))
axis_l = ax.spines['left']
axis_l.set_position(('data', 0))
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
plt.show()
|
:star:图例
显示两条曲线的图例,并测试loc属性。
描述这个图所画的内容
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
plt.plot(xarray, yarray ... label='', ...)
plt.legend(loc='')
如果想要使用legend ,需要在plot画图的时候,指定参数label 可以写latex
|
:star:特殊点
语法:
1
2
3
4
5
6
7
8
9
|
plt.scatter(xarray, yarray,
marker='',
s='',
edgecolor='',
facecolor='',
zorder=3
)
|
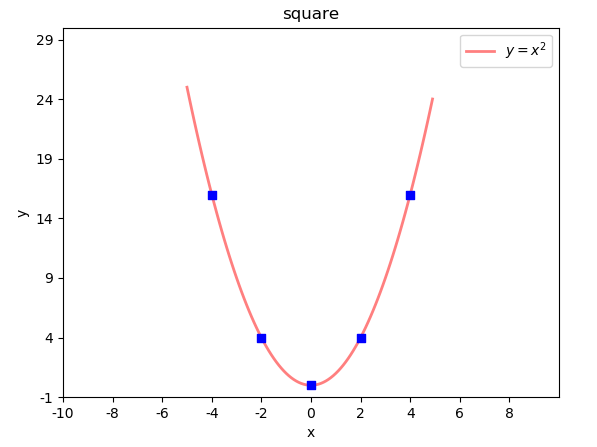
示例:在二次函数图像中添加特殊点
1
2
3
4
5
6
7
|
plt.scatter(x_tck,
x_tck ** 2,
marker="s",
s=40,
facecolor="blue",
zorder=3)
|
marker点型可参照:help(matplotlib.markers)
也可参照附录: matplotlib point样式
:star:备注
语法:
1
2
3
4
5
6
7
8
9
10
|
plt.annotate(
r'$\frac{\pi}{2}$',
xycoords='data',
xy=(x, y),
textcoords='offset points',
xytext=(x, y),
fontsize=14,
arrowprops=dict()
)
|
arrowprops参数使用字典定义指向目标点的箭头样式
1
2
3
4
5
|
arrowprops=dict(
arrowstyle='',
connectionstyle=''
)
|
箭头样式(arrowstyle)字符串如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| ============ =============================================
Name Attrs
============ =============================================
'-' None
'->' head_length=0.4,head_width=0.2
'-[' widthB=1.0,lengthB=0.2,angleB=None
'|-|' widthA=1.0,widthB=1.0
'-|>' head_length=0.4,head_width=0.2
'<-' head_length=0.4,head_width=0.2
'<->' head_length=0.4,head_width=0.2
'<|-' head_length=0.4,head_width=0.2
'<|-|>' head_length=0.4,head_width=0.2
'fancy' head_length=0.4,head_width=0.4,tail_width=0.4
'simple' head_length=0.5,head_width=0.5,tail_width=0.2
'wedge' tail_width=0.3,shrink_factor=0.5
============ =============================================
|
连接线样式(connectionstyle)字符串如下
1
2
3
4
5
6
7
8
9
| ============ =============================================
Name Attrs
============ =============================================
'angle' angleA=90,angleB=0,rad=0.0
'angle3' angleA=90,angleB=0`
'arc' angleA=0,angleB=0,armA=None,armB=None,rad=0.0
'arc3' rad=0.0
'bar' armA=0.0,armB=0.0,fraction=0.3,angle=None
============ =============================================
|
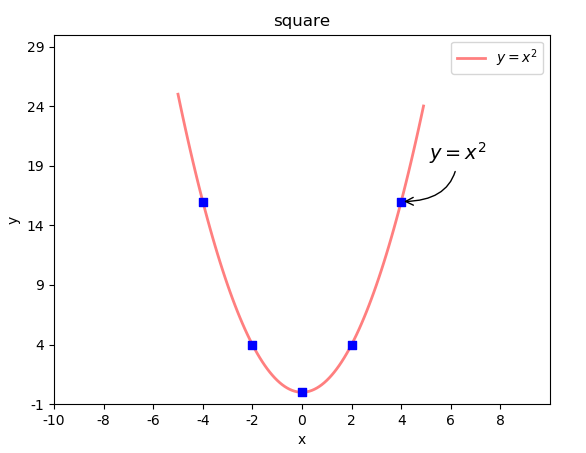
示例:在二次函数图像中添加备注
1
2
3
4
5
6
7
8
9
10
11
12
|
plt.annotate(
r'$y = x ^ 2$',
xycoords='data',
xy=(4, 16),
textcoords='offset points',
xytext=(20, 30),
fontsize=14,
arrowprops=dict(
arrowstyle="->", connectionstyle="angle3"
)
)
|
:star2:高级绘图
语法:绘制两个窗口,一起显示。
1
2
3
4
5
6
7
|
plt.figure(
'sub-fig',
figsize=(4, 3),
facecolor=''
)
plt.show()
|
plt.figure方法不仅可以构建一个新窗口,如果已经构建过title='A’的窗口,又使用figure方法构建了title=‘A’ 的窗口的话,mp将不会创建新的窗口,而是把title='A’的窗口置为当前操作窗口。
设置当前窗口的参数
语法:测试窗口相关参数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
plt.title(title, fontsize=12)
plt.xlabel(x_label_str, fontsize=12)
plt.ylabel(y_label_str, fontsize=12)
plt.tick_params(..., labelsize=8, ...)
plt.grid(linestyle='')
plt.tight_layout()
|
示例:绘制两个图像窗口
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
import matplotlib.pyplot as plt
plt.figure("FigureA", facecolor="lightgray")
plt.grid(linestyle="-.")
plt.figure("FigureB", facecolor="gray")
plt.title('Figure BBB')
plt.xlabel("Date", fontsize=14)
plt.ylabel("Price", fontsize=14)
plt.grid(linestyle="--")
plt.tight_layout()
plt.show()
|
执行结果:
:star:子图 :在一个窗口中,有多个图表
:sparkles:矩阵式布局
(最常用的)
绘制矩阵式子图布局相关API:
1
2
3
4
5
6
7
8
9
10
11
| plt.figure('Subplot Layout', facecolor='lightgray')
plt.subplot(rows, cols, num) 3,3,5
plt.subplot(3, 3, 5)
plt.subplot(335)
|
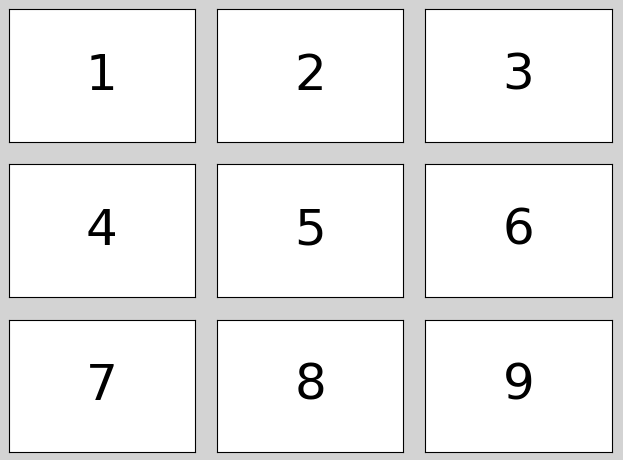
案例:绘制9宫格矩阵式子图,每个子图中写一个数字。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| plt.figure('Subplot Layout', facecolor='lightgray')
for i in range(9):
plt.subplot(3, 3, i+1)
plt.text(
0.5, 0.5, i+1,
ha='center',
va='center',
size=36,
alpha=0.5,
withdash=False
)
plt.xticks([])
plt.yticks([])
plt.tight_layout()
plt.show()
|
执行结果:
:sparkles:网格式布局
网格式布局支持单元格的合并。
绘制网格式子图布局相关API:
1
2
3
4
5
6
7
8
9
10
11
| import matplotlib.gridspec as mg
plt.figure('Grid Layout', facecolor='lightgray')
gs = mg.GridSpec(3, 3)
plt.subplot(gs[0, :2]) [行,列]
plt.text(0.5, 0.5, '1', ha='center', va='center', size=36)
plt.show()
|
案例:绘制一个自定义网格布局。
1
2
3
4
5
6
7
8
9
| import matplotlib.gridspec as mg
plt.figure('GridLayout', facecolor='lightgray')
gridsubs = plt.GridSpec(3, 3)
plt.subplot(gridsubs[0, :2])
plt.text(0.5, 0.5, 1, ha='center', va='center', size=36)
plt.tight_layout()
plt.xticks([])
plt.yticks([])
|
:sparkles:自由式布局
自由式布局相关API:
1
2
3
4
5
6
7
8
9
10
11
12
13
| plt.figure('Flow Layout', facecolor='lightgray')
构建坐标系
plt.axes([0.03, 0.03, 0.94, 0.94]) x,y,width,height
plt.text(0.5, 0.5, '1', ha='center', va='center', size=36)
plt.show()
|
案例:测试自由式布局,定位子图。
1
2
3
4
5
| plt.figure('FlowLayout', facecolor='lightgray')
plt.axes([0.1, 0.2, 0.5, 0.3])
plt.text(0.5, 0.5, 1, ha='center', va='center', size=36)
plt.show()
|
:star:散点图
可以通过每个点的坐标、颜色、大小和形状表示不同的特征值。
散点图可以直观的呈现一组数据的数值分布,从而可以更好的选择合适的数学模型来表达这组数据的数值分布规律。
| 身高 |
体重 |
性别 |
年龄段 |
种族 |
| 180 |
80 |
男 |
中年 |
亚洲 |
| 160 |
50 |
女 |
青少 |
美洲 |
绘制散点图的相关API:
1
2
3
4
5
6
7
8
9
10
11
12
| plt.scatter(
x,
y,
marker='',
s=10,
color='',
edgecolor='',
facecolor='',
zorder=''
)
cmap
|
numpy.random提供了normal函数用于产生符合 正态分布 的随机数
1
2
3
4
5
6
| n = 100
x = np.random.normal(172, 10, n)
y = np.random.normal(60, 10, n)
|
案例:绘制平面散点图。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
import matplotlib.pyplot as plt
import numpy as np
n = 40
x = np.random.normal(172, 20 ,n )
y = np.random.normal(60, 10, n)
x2 = np.random.normal(180, 20 ,n )
y2 = np.random.normal(70, 10, n)
plt.figure("scatter", facecolor="lightgray")
plt.title("Scatter Demo")
plt.scatter(x, y, c="red", marker="D")
plt.scatter(x2, y2, c="blue", marker="v")
plt.xlim(100, 240)
plt.ylim(0, 100)
plt.show()
|
cmap颜色映射表参照:
:star:填充
以某种颜色自动填充两条曲线的闭合区域。
1
2
3
4
5
6
7
8
| plt.fill_between(
x,
sin_x,
cos_x,
sin_x<cos_x,
color='',
alpha=0.2
)
|
案例:绘制两条曲线: sin_x = sin(x) cos_x = cos(x / 2) / 2 [0-8π]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| import matplotlib.pyplot as plt
import numpy as np
n = 1000
x = np.linspace(0, 8 * np.pi, n)
sin_y = np.sin(x)
cos_y = np.cos(x / 2) / 2
plt.figure('Fill', facecolor='lightgray')
plt.title('Fill', fontsize=20)
plt.xlabel('x', fontsize=14)
plt.ylabel('y', fontsize=14)
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(x, sin_y, c='dodgerblue', label=r'$y=sin(x)$')
plt.plot(x, cos_y, c='orangered', label=r'$y=\frac{1}{2}cos(\frac{x}{2})$')
plt.fill_between(x, cos_y, sin_y, cos_y < sin_y, color='dodgerblue', alpha=0.5)
plt.fill_between(x, cos_y, sin_y, cos_y > sin_y, color='orangered', alpha=0.5)
plt.legend()
plt.show()
|
:star:条形图(柱状图) (重点)
最熟悉的
绘制柱状图的相关API: (bar)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
plt.figure('Bar', facecolor='lightgray')
plt.bar(
x,
y,
width,
color='',
label='',
alpha=0.2
)
legend
|
案例:先以柱状图绘制苹果12个月的销量,然后再绘制橘子的销量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| import matplotlib.pyplot as plt
import numpy as np
apples = np.array([30, 25, 22, 36, 21, 29, 20, 24, 33, 19, 27, 15])
oranges = np.array([24, 33, 19, 27, 35, 20, 15, 27, 20, 32, 20, 22])
plt.figure('Bar', facecolor='lightgray')
plt.title('Bar', fontsize=20)
plt.xlabel('Month', fontsize=14)
plt.ylabel('Price', fontsize=14)
plt.tick_params(labelsize=10)
plt.grid(axis='y', linestyle=':')
plt.ylim((0, 40))
x = np.arange(len(apples))
plt.bar(x - 0.2,
apples,
0.4,
color='dodgerblue',
label='Apple')
plt.bar(x + 0.2,
oranges,
0.4,
color='orangered', label='Orange', alpha=0.75)
plt.xticks(x, ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec'])
plt.legend()
plt.show()
|
:star:直方图
执行结果:
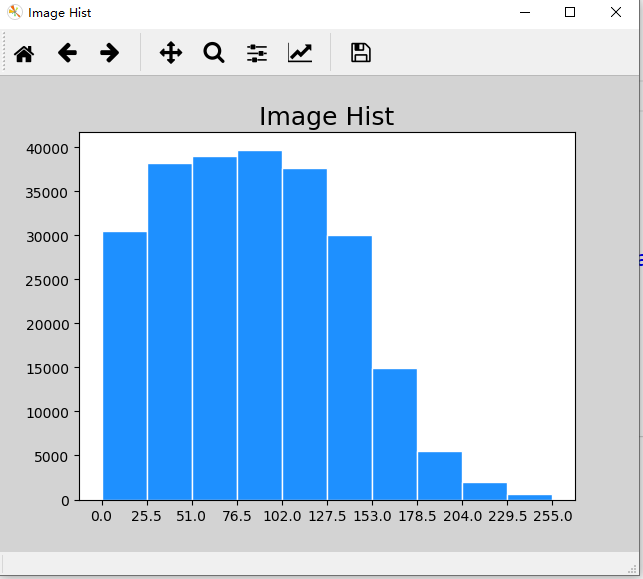
直方图:数值分布的密度
绘制直方图相关API:
1
2
3
4
5
6
7
8
| plt.hist(
x,
bins,
color,
edgecolor
)
|
案例:绘制统计直方图显示图片像素亮度分布:
1
2
3
4
5
6
7
8
9
10
11
12
13
| import numpy as np
import matplotlib.pyplot as plt
import scipy.misc as sm
img = sm.imread('../data/forest.jpg', True)
print(img.shape)
pixes = img.ravel()
plt.figure('Image Hist', facecolor='lightgray')
plt.title('Image Hist', fontsize=18)
plt.xticks(np.linspace(0, 255, 11))
plt.hist(x=pixes, bins=10, color='dodgerblue', range=(0, 255), edgecolor='white', normed=False)
plt.show()
|
:star:扩展:随机数模块与概率分布
numpy提供了random模块生成服从特定统计规律的随机数序列。
一组随机数可能呈现如下分布:
连续性随机变量
统计班级同学体重:[63.2, 76.5, 65.7, 68.9, 59.4 … ]
统计班级同学身高:[163.2, 176.5, 165.7, 168.9, 159.4 … ]
统计班级同学到班时间:[‘07:20:22’,‘07:30:48’,‘07:21:23’,‘07:24:58’ …]
又或者呈现如下分布:
离散型随机变量
统计班级同学体重级别:[偏轻, 中等, 偏重, 超重, 中等, 偏重, 超重, 中等, 偏重…]
统计班级同学身高级别:[偏低, 中等, 中等, 中等, 中等, 偏高, 中等, 中等, 偏高…]
统计最近班级同学迟到人数(共10人):[0, 1, 3, 0, 0, 1, 2, 0, 0, 0 …]
:sparkles:二项分布(binomial)
二项分布就是重复n次独立事件的伯努利试验(Bernoulli experiment)。在每次试验中只有两种可能的结果(进或不进),而且两种结果发生与否互相对立,并且相互独立,事件发生与否的概率在每一次独立试验中都保持不变,例如抛硬币。
1
2
|
np.random.binomial(n, p, size)
|
二项分布可以用于求如下场景的概率的近似值:
- 某人投篮命中率为0.3,投10次,进5个球的概率。
1
2
|
sum(np.random.binomial(10, 0.3, 200000) == 5) / 200000
|
- 某人打客服电话,客服接通率是0.6,一共打了3次,都没人接的概率。
1
| sum(np.random.binomial(3, 0.6, 200000) == 0) / 200000
|
示例:模拟某人以30%命中率投篮,每次投10个,计算并打每种进球可能的概率
1
2
3
4
5
6
7
8
9
10
|
import numpy as np
import matplotlib.pyplot as mp
r = np.random.binomial(10, 0.5, 200000)
mp.hist(r, 11, edgecolor='white')
mp.legend()
mp.show()
|
执行结果:
:sparkles:超几何分布(hypergeometric)
超几何分布是统计学上一种离散概率分布。它描述了从有限N个物件(其中包含M个指定种类的物件)中拿出出n个物件,其中指定种类的物件的数量(也就是说抽出不放回)。以下是一组超几何分布的示例:
(1)10件产品中含有3件次品,从中任意取4件产品,所取出的次品件数服从超几何分布;
(2)袋中有8红球4白球,从中任意摸出5个球,摸出红球个数服从超几何分布;
(3)某班45个学生,女生20人,现从中选7人做代表,代表中所含女生的人数服从超几何分布;
(4)15张卡片中含有5件写有“奖”字,从中任意取3件产品,所取出的卡片中含有奖字的卡片张数服从超几何分布;
(5)10位代表中有5位支持候选人A,随机采访3人,其中支持候选人A的人数服从超几何分布;
(6)盘中装有10个粽子,豆沙粽2个,肉粽3个,白粽5个,从中任选3个,取到的豆沙粽的个数服从超几何分布。
API介绍:
1
2
|
np.random.hypergeometric(ngood(2), nbad(8), nsample(3), size(10))
|
示例一:从6个好苹果、4个坏苹果中抽取3个苹果,返回好苹果的数量(执行10次)
1
2
3
4
5
6
| import numpy as np
n = np.random.hypergeometric(6, 4, 3, 10)
print(n)
print(n.mean())
|
:sparkles:正态分布(normal)
1
2
3
4
|
np.random.normal(size)
np.random.normal(loc=1, scale=10, size)
|
$$
\text{标准正态分布概率密度:} \frac{e^{-\frac{x^2}{2}}}{\sqrt{2\pi}}
$$
案例:生成10000个服从正态分布的随机数并绘制随机值的频数直方图。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| import numpy as np
import matplotlib.pyplot as mp
samples = np.random.normal(size=10000)
mp.figure('Normal Distribution',facecolor='lightgray')
mp.title('Normal Distribution', fontsize=20)
mp.xlabel('Sample', fontsize=14)
mp.ylabel('Occurrence', fontsize=14)
mp.tick_params(labelsize=12)
mp.grid(axis='y', linestyle=':')
mp.hist(samples, 100, edgecolor='steelblue',
facecolor='deepskyblue', label='Normal')
mp.legend()
mp.show()
|
:star:饼图
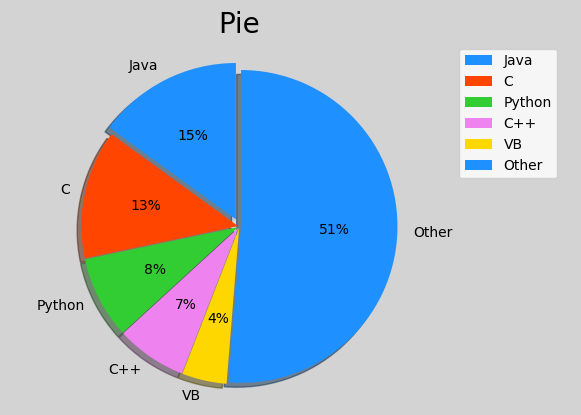
绘制饼状图的基本API:
1
2
3
4
5
6
7
8
9
10
| plt.pie(
values,
spaces,
labels,
colors,
'%d%%',
shadow=True,
startangle=90
radius=1
)
|
案例:绘制饼状图显示6门编程语言的流行程度:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| import matplotlib.pyplot as plt
import numpy as np
plt.figure('pie', facecolor='lightgray')
plt.title('Pie', fontsize=20)
values = [15, 13.3, 8.5, 7.3, 4.62, 51.28]
spaces = [0.05, 0.01, 0.01, 0.01, 0.01, 0.01]
labels = ['Java', 'C', 'Python', 'C++', 'VB', 'Other']
colors = ['dodgerblue', 'orangered', 'limegreen', 'violet', 'gold','blue']
plt.axis('equal')
plt.pie(
values,
spaces,
labels,
colors,
'%d%%',
shadow=True,
startangle=90,
radius=1
)
plt.legend()
plt.show()
|














