注:封面画师:新雨林-触站
说明
- 本页面无手机端适配,强制缩放阅读。
- 使用纯html格式,保存教学用ppt,添加了部分个人笔记。
- 目录工作正常,可以跳转。
损失函数与梯度下降
损失函数与梯度下降
损失函数
损失函数的作用
什么是损失函数
梯度下降
常用的损失函数
什么是梯度
梯度下降
导数与偏导数
学习率
梯度递减训练法则
梯度下降算法
损失函数

知
识
讲
解
什么是损失函数
• 损失函数(Loss Function),也有称之为代价函数(Cost Function),
用
来度量预测值和实际值之间的差异。

知
识
讲
解
损失函数的作用
• 度量决策函数f(x)和实际值之间的差异。
• 作为模型性能参考。损失函数值越小,说明预测输出和实际结果(也称期望
输出)之间的差值就越小,也就说明我们构建的模型越好。
学习的过程,就
是不断通过训练数据进行预测,不断调整预测输出与实际输出差异,使的损
失值最小的过程。
知
识
讲
解
常用损失函数
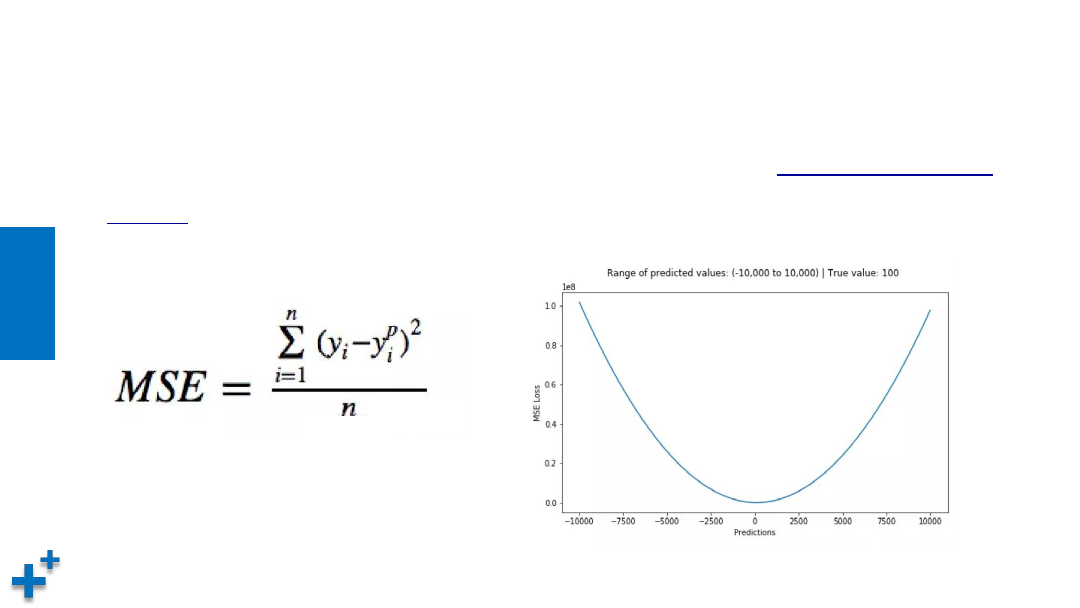
• 均方误差(Mean square error)损失函数。均方误差是
回归问题常用的损
失函数
,它是预测值与目标值之间差值的平方和,其公式和图像如下所示:
知
识
讲
解
常用损失函数(续1)
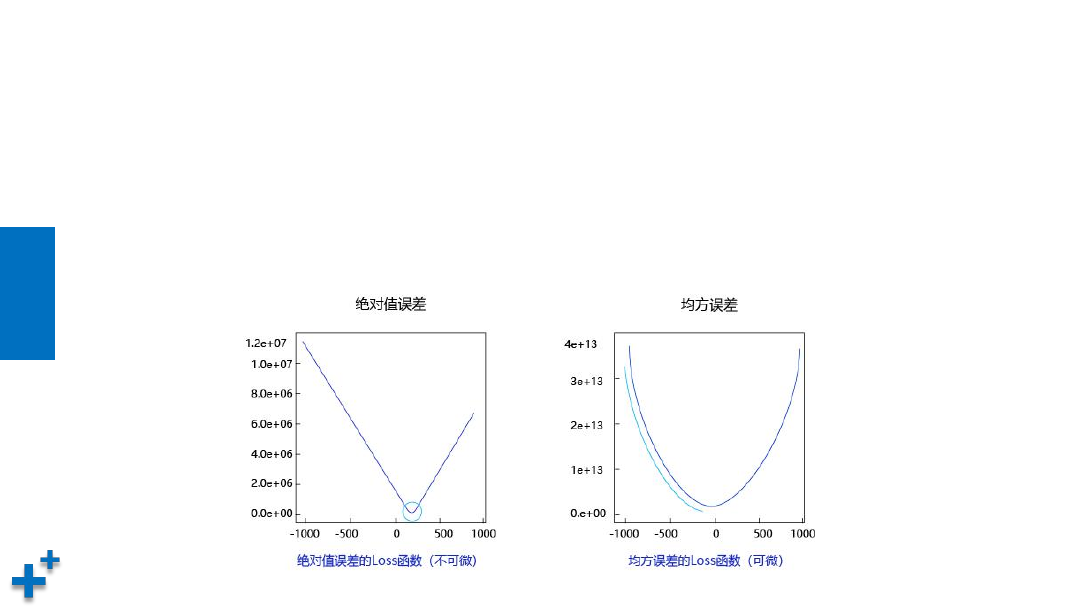
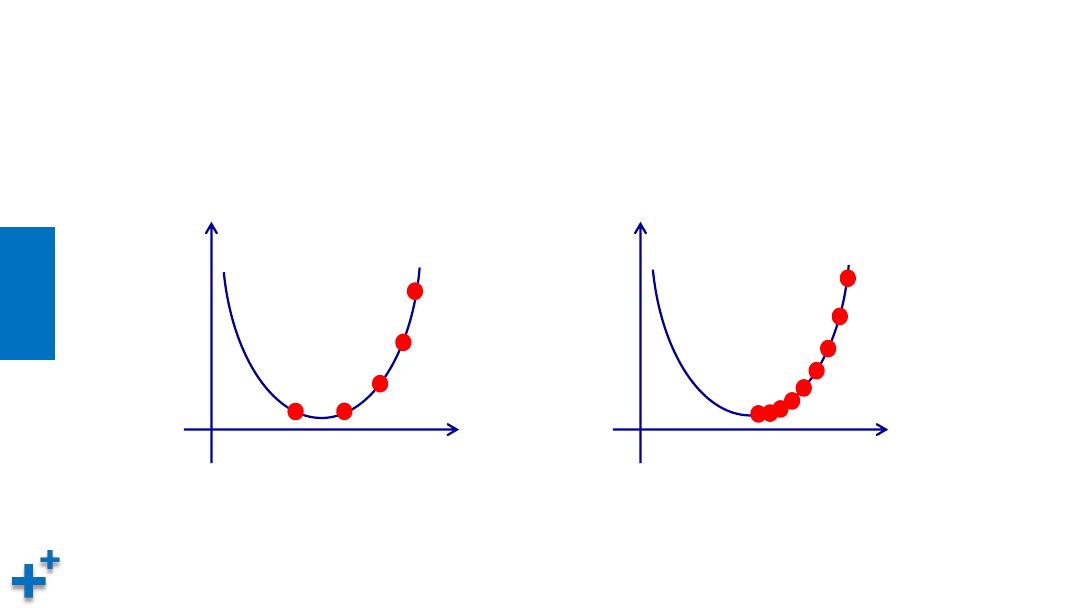
为什么使用误差的平方
• 曲线的最低点是可导的
• 越接近最低点,曲线的坡度逐渐放缓,有助于通过当前的梯度来判断接近最低点的程
度(是否逐渐减少步长,以免错过最低点)
知
识
讲
解
常用损失函数(续2)
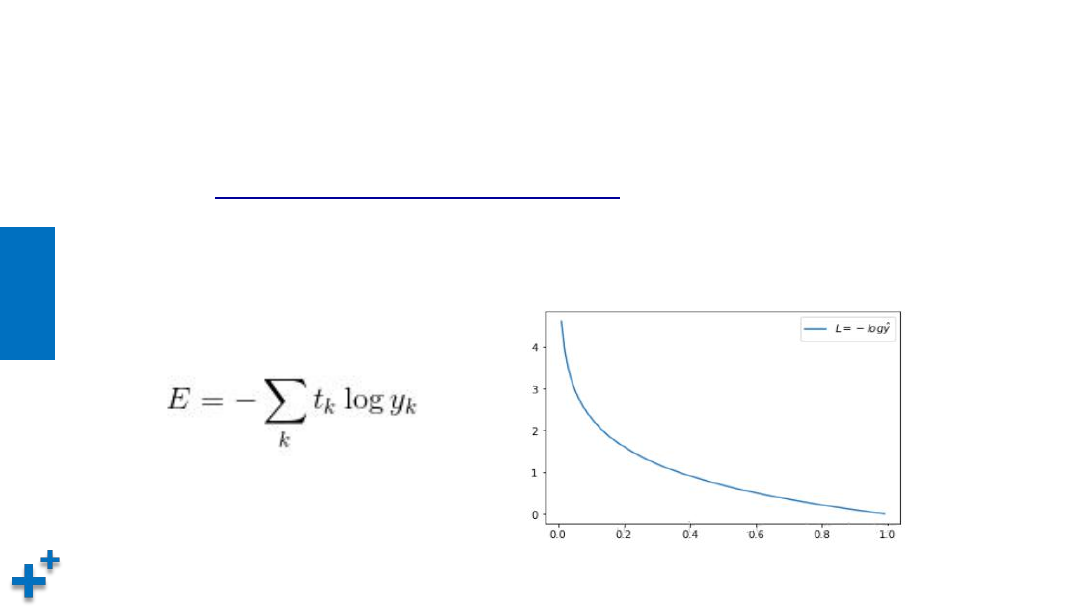
• 交叉熵(Cross Entropy)。交叉熵是Shannon信息论中一个重要概念,
主要用于
度量两个概率分布间的差异性信息
,在机器学习中用来作为分类
问题的损失函数。假设有两个概率分布,t
k
与y
k
,其交叉熵函数公式及图形
如下所示:
梯度下降
知
识
讲
解
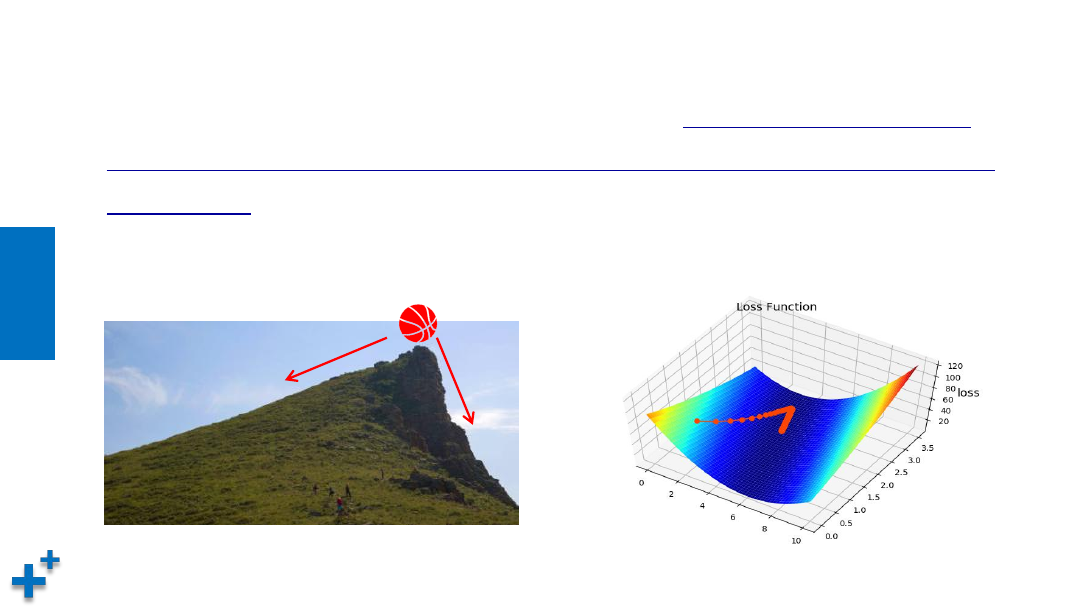
什么是梯度
• 梯度(gradient)是一个向量(矢量,有方向),表示
某一函数在该点处的方向导
数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,
变化率最大。
损失函数沿梯度相反方向收敛最快(即能最快找到极值点)。当梯度
向量为零(或接近于零),说明损失函数到达一个极小值点,模型准确度达到一个
极大值点。
快
慢

知
识
讲
解
梯度下降
• 通过损失函数,我们将“寻找最优参数”问题,转换为了“寻找损失函数
最小值”问题。
寻找步骤:
(1)损失是否足够小?如果不是,计算损失函数的梯度。
(2)按梯度的反方向走一小步,以缩小损失。
(3)循环到(1)。
这种按照负梯度不停地调整函数权值的过程就叫作“
梯度下降法
”。通过这样的方法,
改变每个神经元与其他神经元的连接权重及自身的偏置,让损失函数的值下降得更快,
进而将值收敛到损失函数的某个极小值。
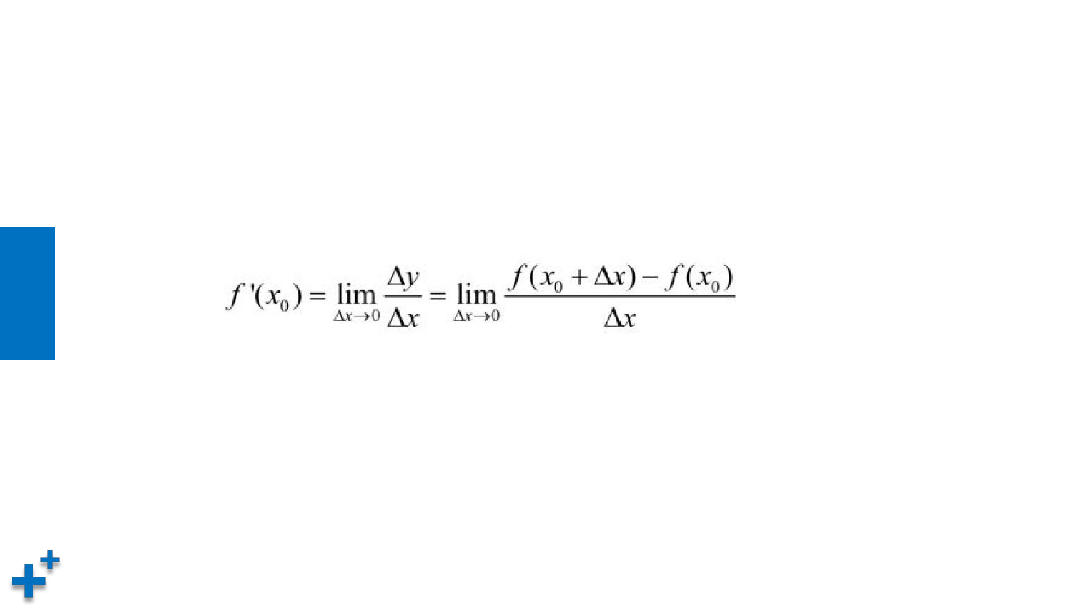
知
识
讲
解
导数与偏导数
• 导数的定义
所谓导数,就是用来分析函数“变化率”的一种度量。其公式为:
知
识
讲
解
导数与偏导数(续1)
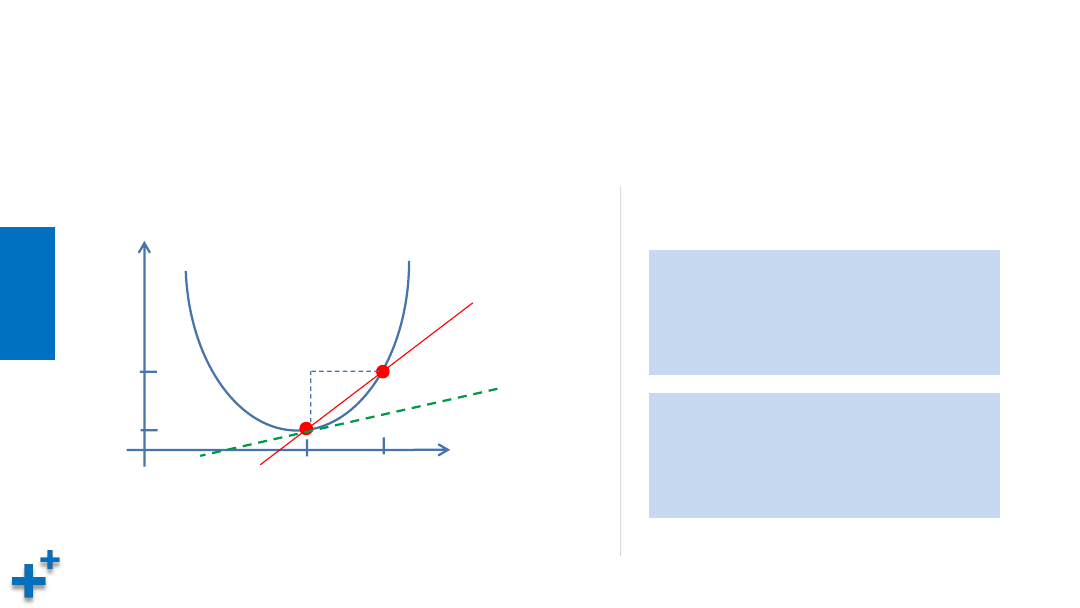
• 导数的含义:反映变化的剧烈程度(变化率)
x
y
x
0
x
1
Δx
Δy
切线斜率
即为该点导数
y
0
y
1
例如:y = x
2
+ 1
x
0
=1 y
0
=2
x
1
= 1.0001 y
1
=2.00020001
∆y / ∆x ≈ 0.0002 / 0.0001 = 2
x
0
=2 y
0
=5
x
1
= 2.0001 y
1
=5.00040001
∆y / ∆x ≈ 0.0004 / 0.0001 = 4
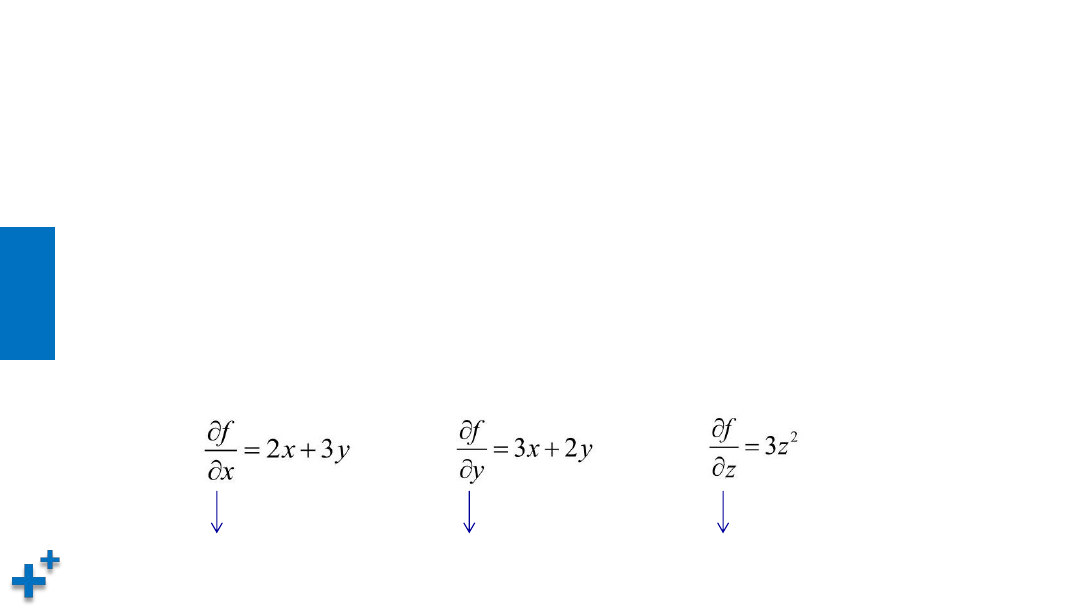
知
识
讲
解
导数与偏导数(续2)
• 偏导数
“偏导”的英文本意是“partial derivatives“(表示局部导数)。对于多维变量函数
而言,当求某个变量的导数时,就是把其他变量视为常量,然后对整个函数求其导数
(相比于全部变量,这里只求一个变量,即为“局部”)。例如有函数:
f = x
2
+ 3xy + y
2
+ z
3
则,对x, y, z分别求偏导公式为:
y, z为常量
x, z为常量
x, y为常量
知
识
讲
解
学习率
• 学习率是梯度下降过程中,在梯度值前面的系数,用来控制调整的步幅大小
收敛步幅过大
通过学习率控制收敛步幅
知
识
讲
解
梯度递减训练法则
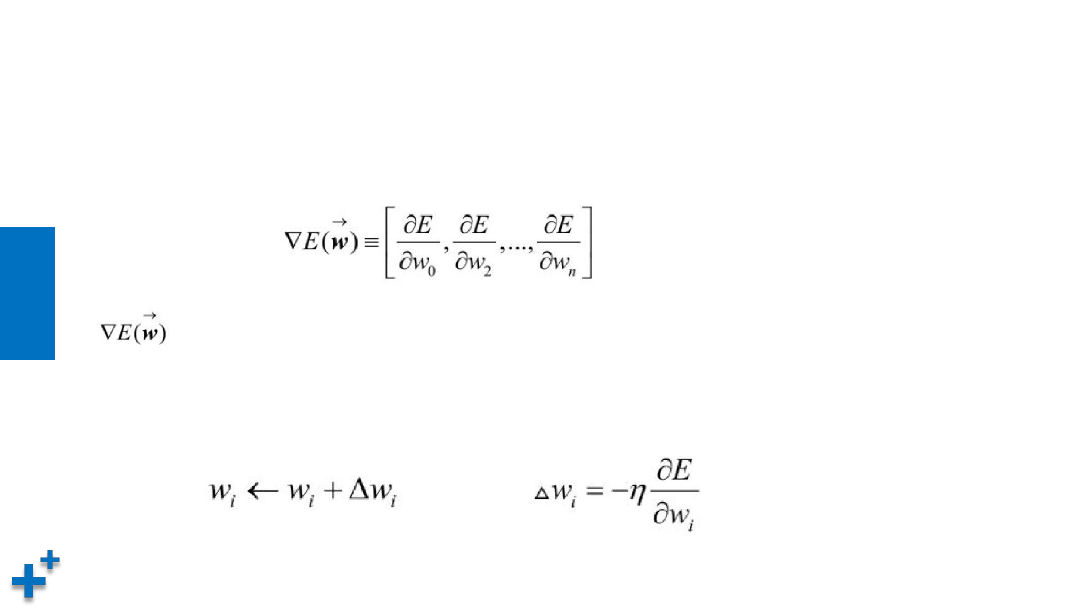
• 神经网络中的权值参数是非常多的,因此针对损失函数E的权值向量的梯度如以下公
式所示:
表示损失函数E的梯度,它本身也是一个向量,它的多个维度分别由损失函数
E对多个权值参数w
i
求偏导所得。当梯度被解释为权值空间中的一个向量时,它就确
定了E陡峭上升的方向,那么梯度递减的训练法则就如下公式所示:

知
识
讲
解
梯度下降算法
• 批量梯度下降
批量梯度下降法(Batch Gradient Descent,BGD)是最原始的形式,它是指在每一次
迭代时使用所有样本来进行梯度的更新。
Ø
优点:
ü
一次迭代是对所有样本进行计算,此时利用矩阵进行操作,实现了并行。
ü
由全数据集确定的方向能够更好地代表样本总体,从而更准确地朝向极值所在的方向。
当目标函数为凸函数时,BGD一定能够得到全局最优。
Ø
缺点:
ü
当样本数目 m 很大时,每迭代一步都需要对所有样本计算,训练过程会很慢。

知
识
讲
解
梯度下降算法(续1)
• 随机梯度下降
随机梯度下降法(Stochastic Gradient Descent,SGD)每次迭代使用一个样本来对
参数进行更新,使得训练速度加快。
Ø
优点:
ü
由于不是在全部训练数据上的损失函数,而是在每轮迭代中,随机优化某一条训练数
据上的损失函数,这样每一轮参数的更新速度大大加快。
Ø
缺点:
ü
准确度下降。由于即使在目标函数为强凸函数的情况下,SGD仍旧无法做到线性收敛。
ü
可能会收敛到局部最优,由于单个样本并不能代表全体样本的趋势。
ü
不易于并行实现。

知
识
讲
解
梯度下降算法(续2)
• 小批量梯度下降
小批量梯度下降(Mini-Batch Gradient Descent, MBGD)是对批量梯度下降以及随
机梯度下降的一个折中办法。其思想是:每次迭代 使用指定个(batch_size)样本来对
参数进行更新。
Ø
优点:
ü
通过矩阵运算,每次在一个batch上优化神经网络参数并不会比单个数据慢太多。
ü
每次使用一个batch可以大大减小收敛所需要的迭代次数,同时可以使收敛到的结果更
加接近梯度下降的效果。
Ø
缺点:
ü
batch_size的不当选择可能会带来一些问题。
知
识
讲
解
梯度下降算法(续3)
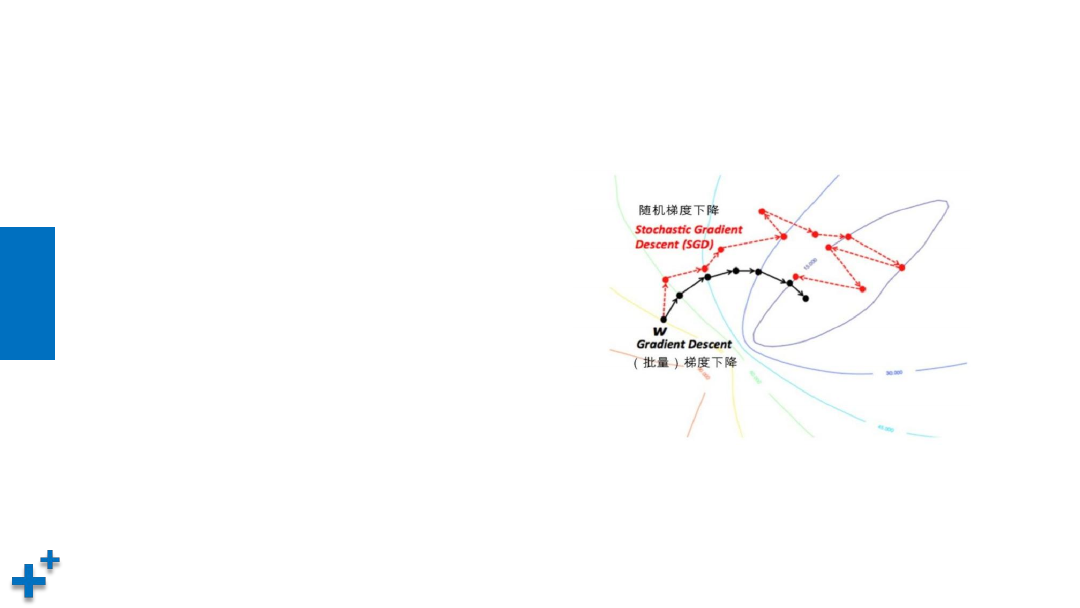
• 几种梯度下降算法收敛比较
Ø
批量梯度下降稳健地向着最低点前进
的
Ø
随机梯度下降震荡明显,但总体上向
最低点逼近
Ø
小批量梯度下降位于两者之间
小结
• 本章节介绍了损失函数与梯度下降概念与算法
ü
损失函数。
用于度量预测值和期望值之间的差异,根据该差异值进行参数调整
ü
梯度下降。
用于以最快的速度、最少的步骤快速找到损失函数的极小值





