注:封面画师:新雨林-触站
说明
- 本页面无手机端适配,强制缩放阅读。
- 使用纯html格式,保存教学用ppt,添加了部分个人笔记。
- 目录工作正常,可以跳转。
感知机与神经网络
感知机与神经网络
感知机
感知机的功能
什么是感知机
如何实现感知机
激活函数
感知机的缺陷
多层感知机
神经网络
什么是神经网络
神经网络的功能
通用近似定理
什么是激活函数
为什么使用激活函数
深层网络的优点
常见激活函数
感知机
知
识
讲
解
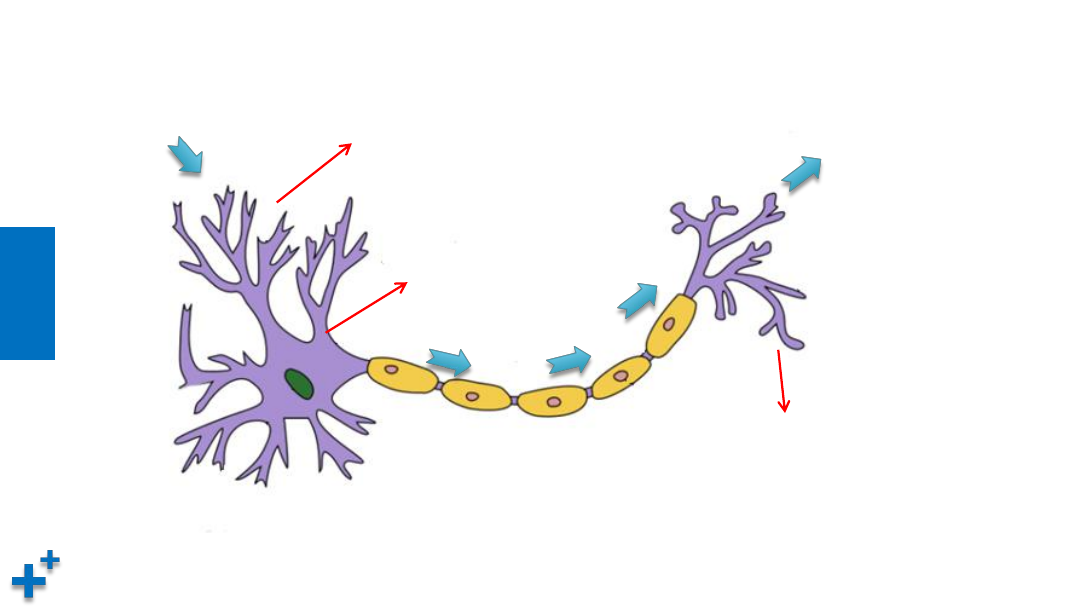
生物神经元
细胞体
(处理信息)
树突(收集信息)
轴突(传递信息)
突触
(输出信息)
知
识
讲
解
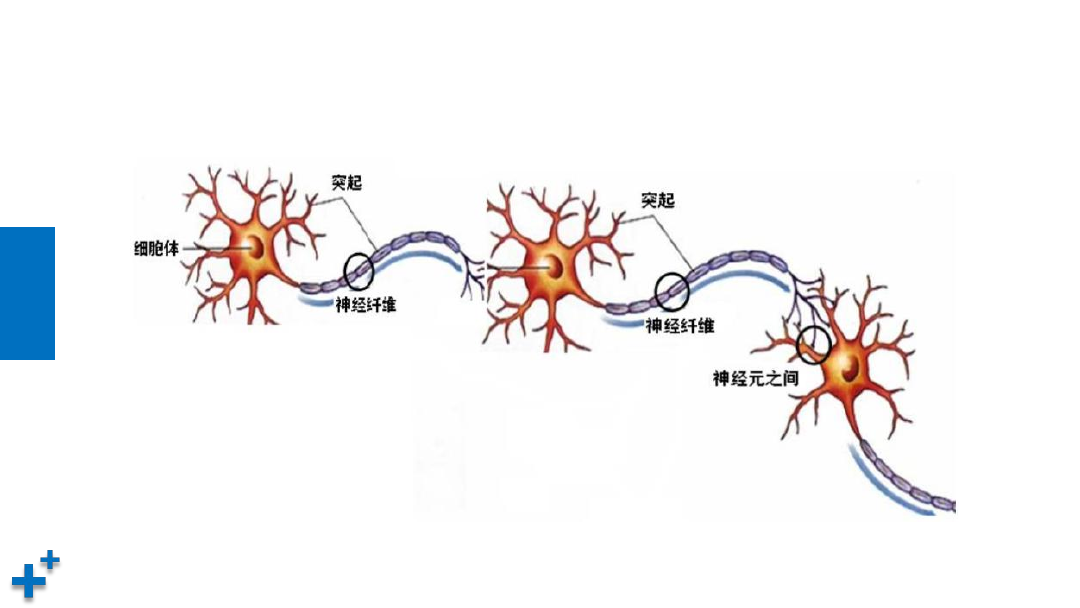
生物神经网络
知
识
讲
解
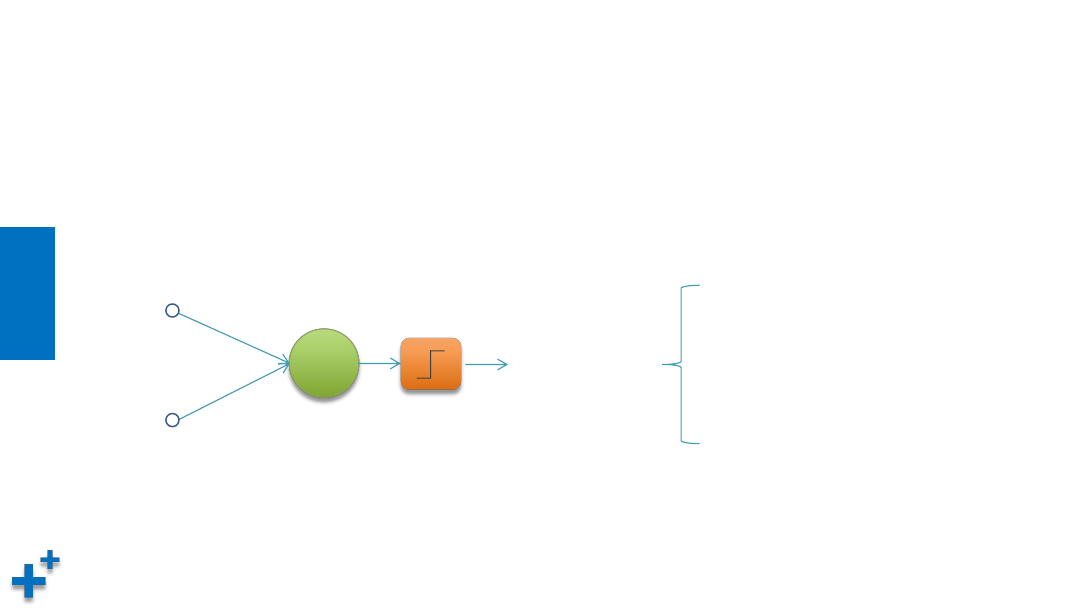
什么是感知机
• 感知机(Perceptron),又称神经元(Neuron,对生物神经元进行了模仿)是神
经网络(深度学习)的起源算法,1958年由康奈尔大学心理学教授弗兰克·罗森布拉
特(Frank Rosenblatt)提出,它可以接收多个输入信号,产生一个输出信号。
+
w
1
w
2
y =
0 (w
1
x
1
+ w
2
x
2
<= θ)
1 (w
1
x
1
+ w
2
x
2
> θ)
其中,x
1
和x
2
称为输入,w
1
和w
2
为权重,
θ为阈值,y为输出
y
θ
x
1
x
2
知
识
讲
解
什么是感知机(续1)
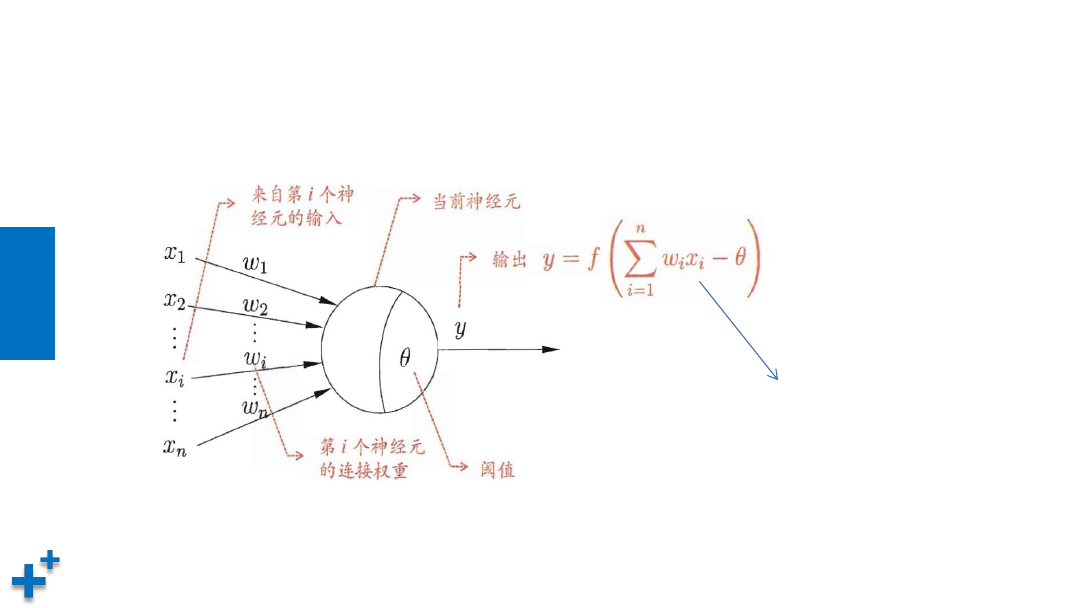
• 神经元更通用的图形表示和表达式
y =f ( w
1
x
1
+ w
2
x
2
+ ... + w
n
x
n
-
θ )
展开

知
识
讲
解
感知机的功能
Ø
作为分类器/回归器,实现自我学习
Ø
实现逻辑运算,包括逻辑和(AND)、逻辑或(OR)
Ø
组成神经网络
知
识
讲
解
感知机的功能(续1)
+
w
1
w
2
一个连续值
(回归器)
θ
x
1
x
2
+
w
1
w
2
多个离散值
(分类器)
x
1
x
2
• 神经元作为回归器 / 分类器
知
识
讲
解
感知机功能(续2)
• 实现逻辑和
0.5
0.5
θ = 0.7
1
+
0.5
0.5
θ = 0.7
0
1
1
+
1
0
0.5
0.5
θ = 0.7
感冒
+
0.5
0.5
θ = 0.7
非感冒
发
烧
咳
嗽
+
发
烧
咳
嗽
1
1
1
0
知
识
讲
解
感知机功能(续3)
• 实现逻辑或
0.5
0.5
θ = 0.2
1
+
0.5
0.5
θ = 0.2
1
1
1
+
1
0
0.5
0.5
θ = 0.2
上医院
+
0.5
0.5
θ = 0.2
上医院
生
病
体
检
+
生
病
体
检
1
1
1
0

知
识
讲
解
如何实现感知机
• 实现逻辑和

知
识
讲
解
• 实现逻辑或
如何实现感知机(续)
知
识
讲
解
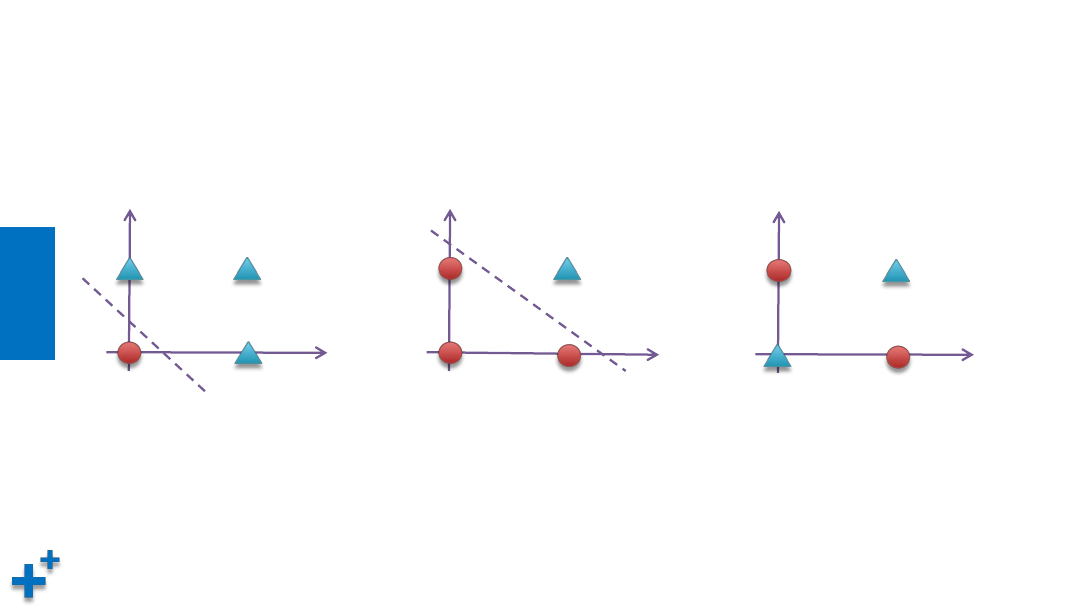
感知机的缺陷
• 感知机的局限在于无法处理“异或”问题(非线性问题)
(0,0)
(1,0)
(0,1)
(1,1)
或门
x
1
x
2
(0,0)
(1,0)
(0,1)
(1,1)
与门
x
1
x
2
(0,0)
(1,0)
(0,1)
(1,1)
异或门
x
1
x
2
知
识
讲
解
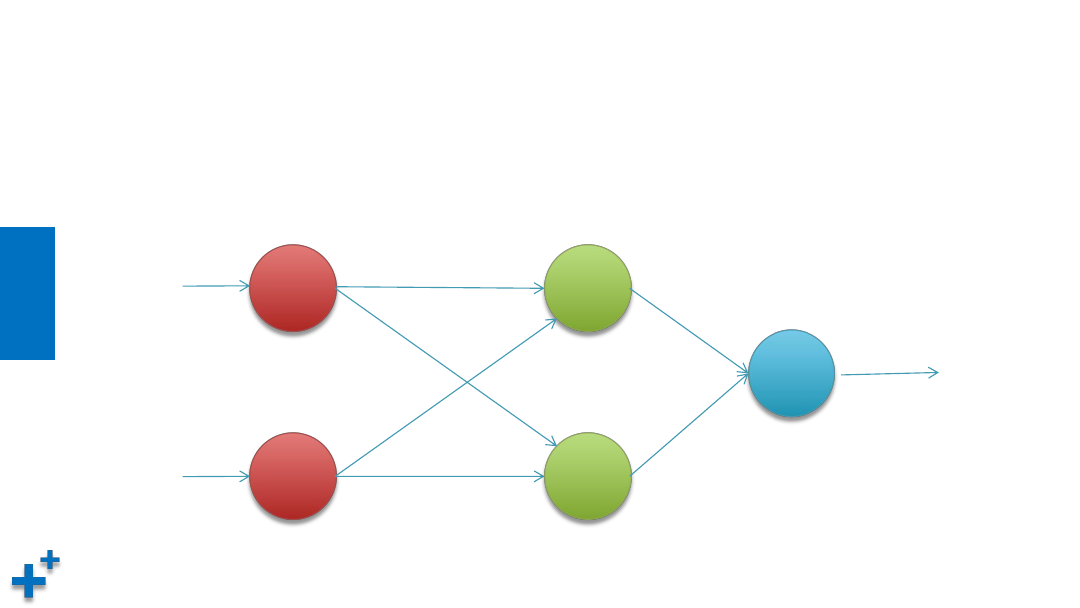
多层感知机
• 1975年,感知机的“异或”难题才被理论界彻底解决,即通过多个感知机组合来解
决该问题,这种模型也叫多层感知机(Multi-Layer Perceptron,MLP)。如下图所
示,神经元节点阈值均设置为0.5
x
0
x
1
w
1
= 1
w
2
= -1
w
3
=
-1
w
4
= 1
y
w
5
= 1
w
6
=
1
1
0
1
输入层
隐含层
输出层
θ = 0.5
θ = 0.5
θ = 0.5

知
识
讲
解
多层感知机(续)
• 多层感知机解决异或门实现
神经网络
知
识
讲
解
什么是神经网络
• 感知机由于结构简单,完成的功能十分有限。可以将若干个感知机连在一起,形成
一个级联网络结构,这个结构称为“多层前馈神经网络”(Multi-layer
Feedforward Neural Networks)。所谓“前馈”是指将前一层的输出作为后一
层的输入的逻辑结构。每一层神经元仅与下一层的神经元全连接。但在同一层之内,
神经元彼此不连接,而且跨层之间的神经元,彼此也不相连。

知
识
讲
解
神经网络的功能
• 1989年,奥地利学者库尔特·霍尼克(Kurt Hornik)等人发表论文证明,
对
于任意复杂度的连续波莱尔可测函数(Borel Measurable Function)f,仅
仅需要一个隐含层,只要这个隐含层包括足够多的神经元,前馈神经网络使
用挤压函数(Squashing Function)作为激活函数,就可以以任意精度来近
似模拟f。
如果想增加f的近似精度,单纯依靠增加神经元的数目即可实现。
• 这个定理也被称为
通用近似定理
(Universal Approximation Theorem),
该定理表明,
前馈神经网在理论上可近似解决任何问题。
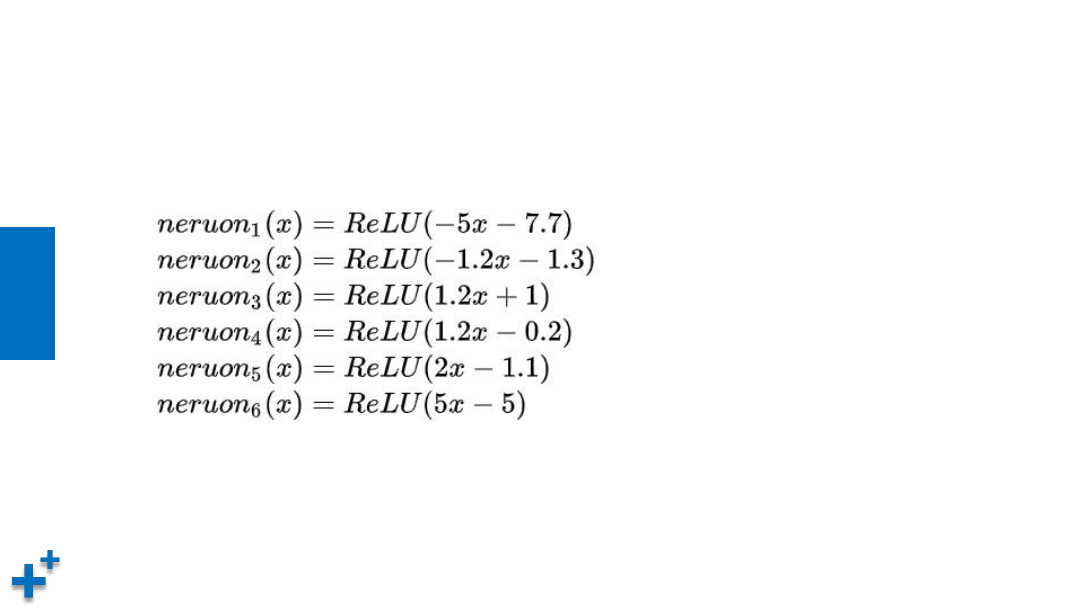
知
识
讲
解
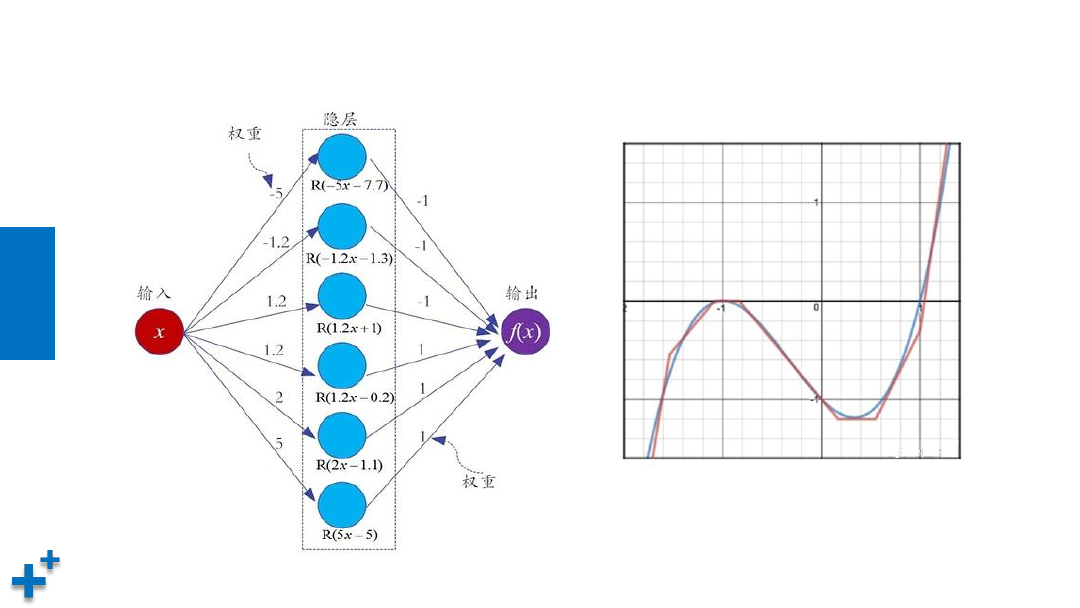
通用近似定理
现有目标函数 f(x) = x
3
+ x
2
- x - 1
,
可以使用6个神经元进行模拟:
知
识
讲
解
通用近似定理(续1)
知
识
讲
解
通用近似定理(续2)
f ( )
猫
f ( )
Hello, deep learning
f ( “
哈哈哈哈
” )
高兴

知
识
讲
解
深层网络的优点
• 其实,神经网络的结构还有另外一个“进化”方向,那就是朝着“纵
深”方向发展,也就是说,减少单层的神经元数量,而增加神经网络
的层数,也就是“深”而“瘦”的网络模型。
• 微软研究院的科研人员就以上两类网络性能展开了实验,
实验结果表
明:增加网络的层数会显著提升神经网络系统的学习性能。
知
识
讲
解
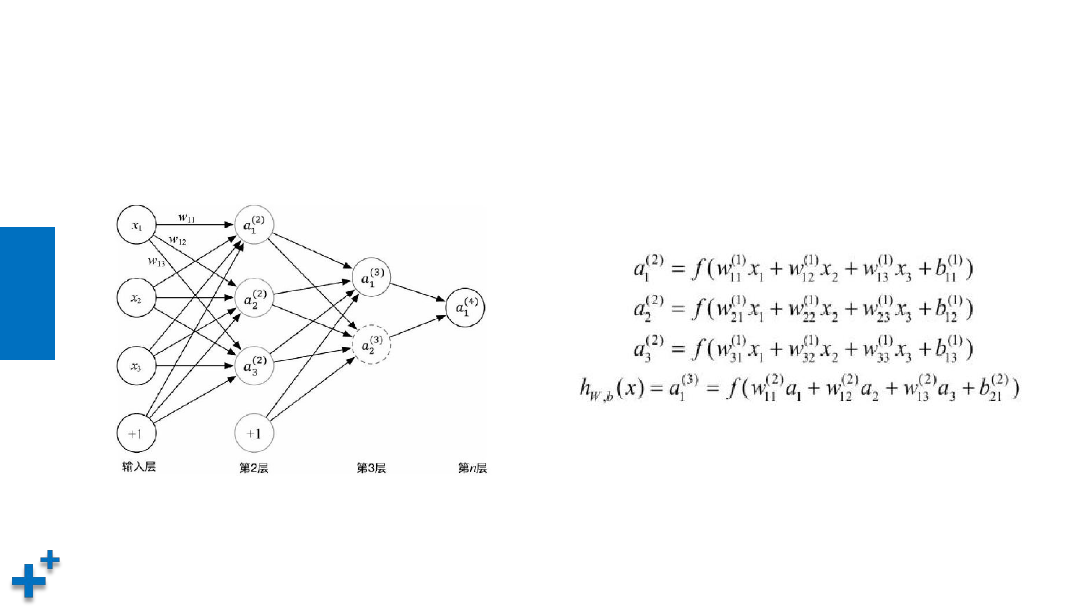
多层神经网络计算公式
知
识
讲
解
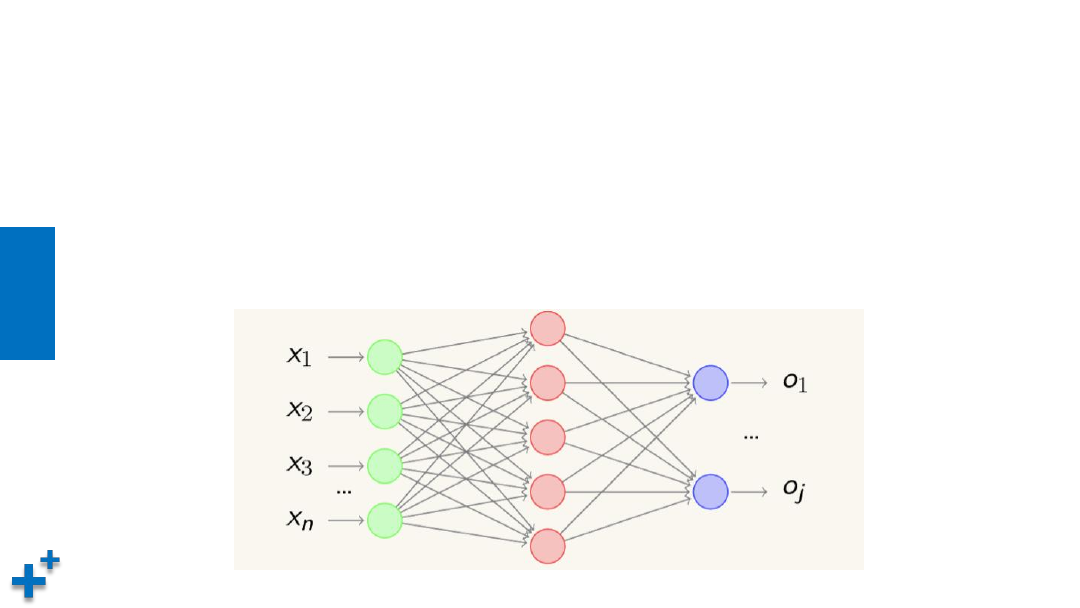
多层神经网络计算公式(续)
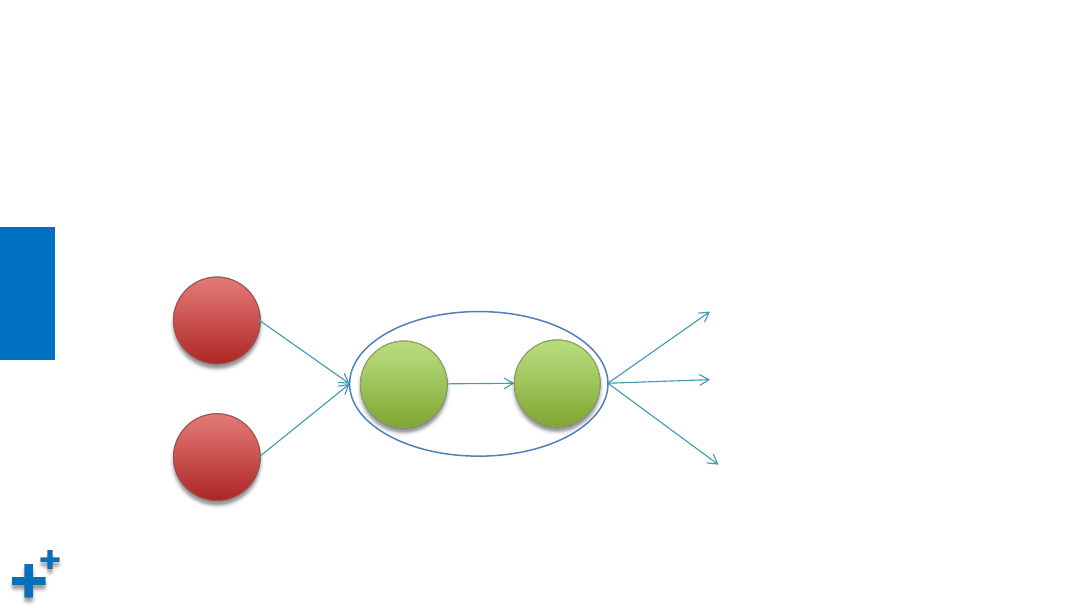
• 以下是一个多层神经网络及其计算公式

激活函数
知
识
讲
解
什么是激活函数
• 在神经网络中,将输入信号的总和转换为输出信号的函数被称为激活
函数(activation function)
x
1
x
2
a
w
1
w
2
h(x)
y
A
B
C

知
识
讲
解
为什么使用激活函数
• 激活函数将多层感知机输出转换为非线性,使得神经网络可以任意
逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模
型中。
• 如果一个多层网络,使用连续函数作为激活函数的多层网络,称之
为“神经网络”,否则称为“多层感知机”。所以,激活函数是区
别多层感知机和神经网络的依据。
知
识
讲
解
常见激活函数
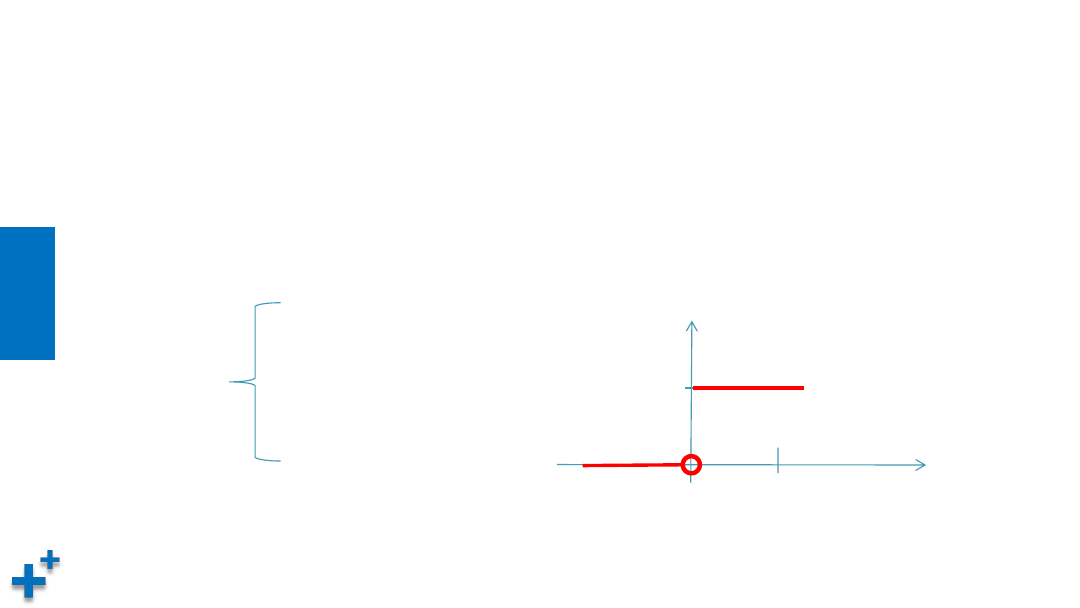
• 阶跃函数
– 阶跃函数(Step Function)是一种特殊的连续时间函数,是一个从0跳变到1的
过程,函数形式与图像:
f(x) =
1 (x >= 0)
0 (x < 0)
x
y
0
1
1
知
识
讲
解
常见激活函数(续1)
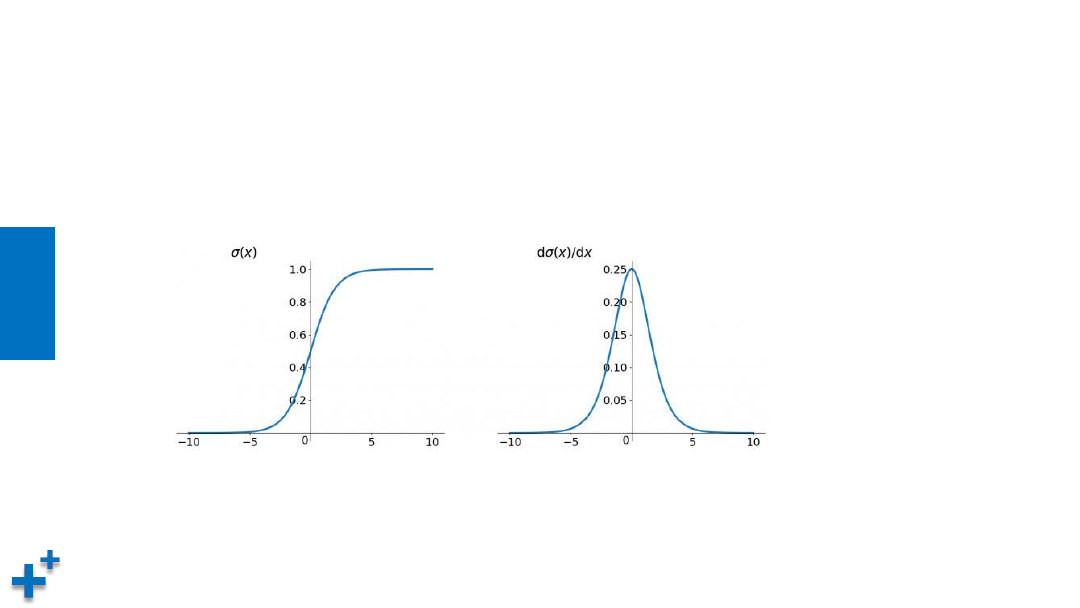
• sigmoid函数
– sigmoid函数也叫Logistic函数,用于隐层神经元输出,取值范围为(0,1),它可以将一个实
数映射到(0,1)的区间,可以用来做二分类,表达式:σ(x) = 1 / (1 + e
-x
)
优点:平滑、易于求导
缺点:激活函数计算量大,反向传播求误差梯度时,求导涉及除法;反向传播时,很容易就
会出现梯度消失的情况,从而无法完成深层网络的训练
知
识
讲
解
常见激活函数(续2)
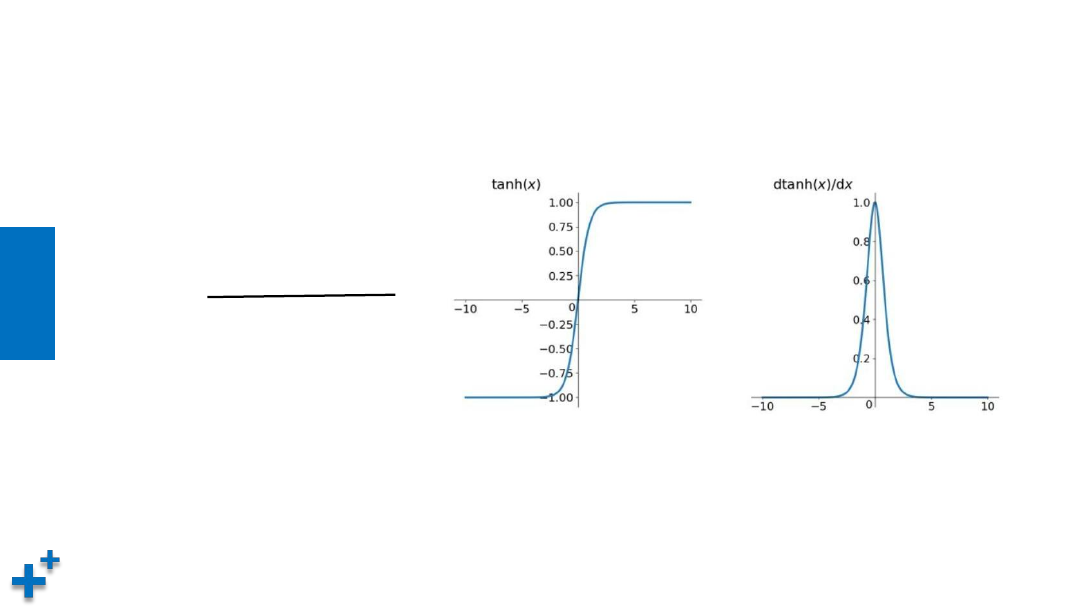
• tanh双曲正切函数
tanh(x) =
1 + e
-2x
1 - e
-2x
优点:平滑、易于求导;输出均值为0,收敛速度要比sigmoid快,从而可以减少迭代次数
缺点:梯度消失
用途:常用于NLP中
知
识
讲
解
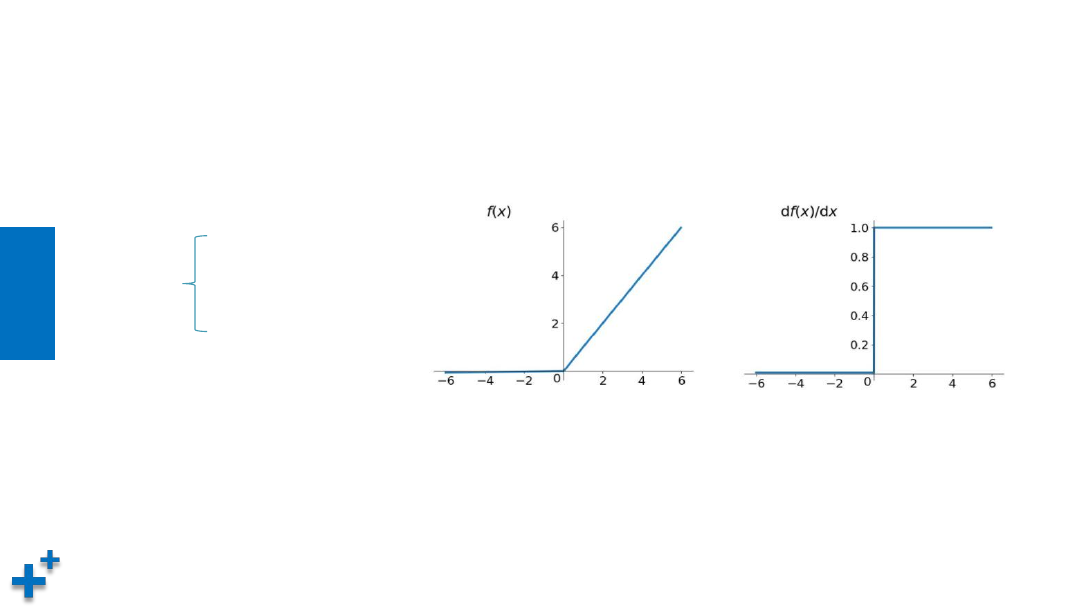
常见激活函数(续3)
• ReLU(Rectified Linear Units,修正线性单元)
优点:(1)更加有效率的梯度下降以及反向传播,避免了梯度爆炸和梯度消失问题
(2)计算过程简单
缺点:小于等于0的部分梯度为0
用途:常用于图像
f(x) =
x (x > 0)
0 (x <= 0)
知
识
讲
解
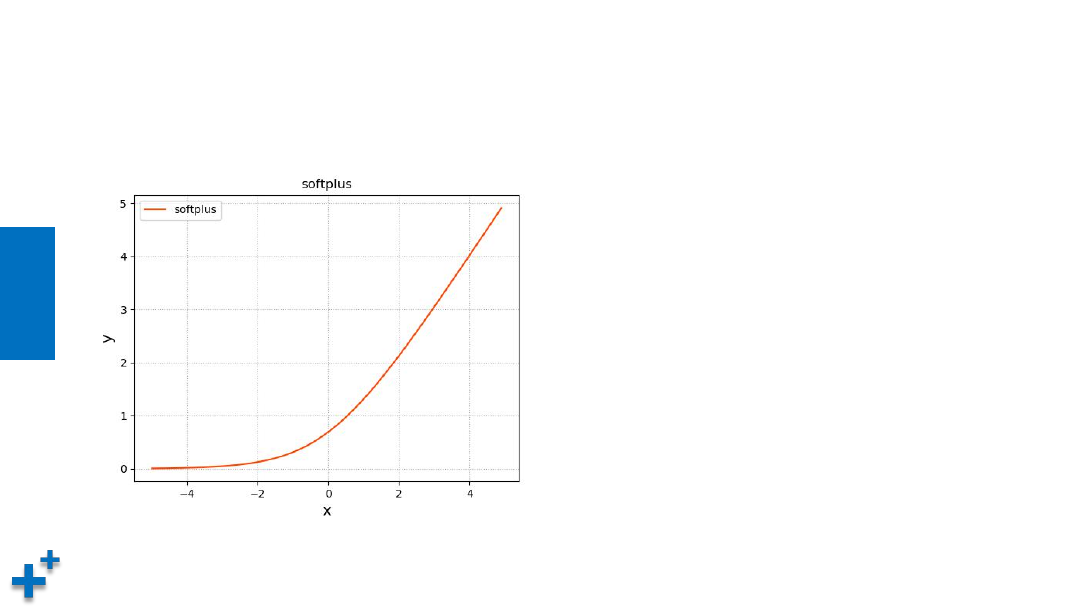
常见激活函数(续4)
• Softplus
Softplus 是对ReLU的平滑逼近解析形
式,更巧的是,Softplus函数的导数
恰好就是Sigmoid函数。但实际应用
效果不如ReLU好
f(x) = ln(1 + e
x
)
知
识
讲
解
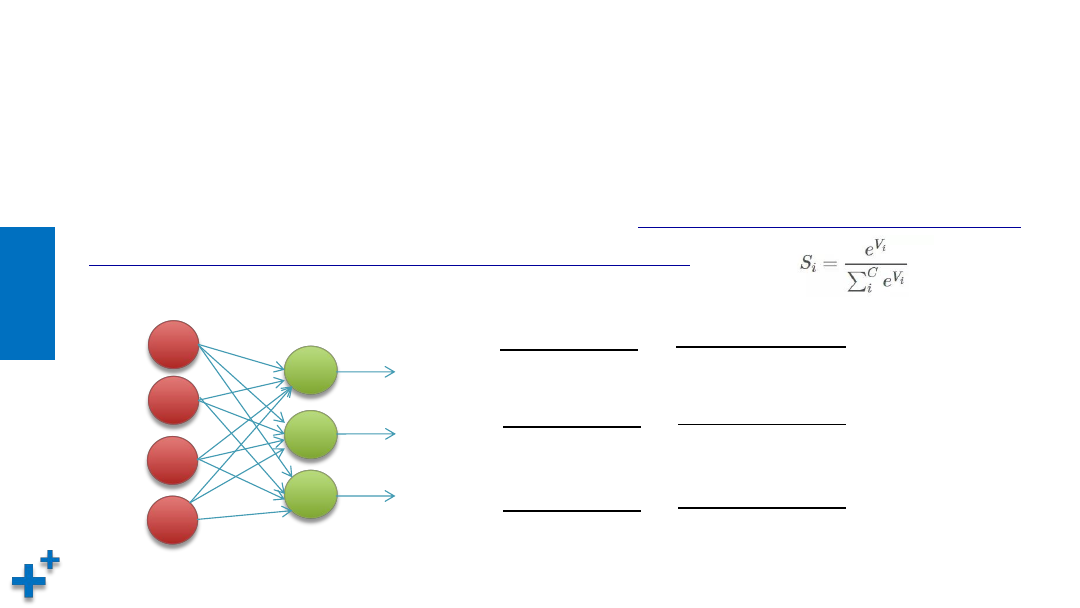
常见激活函数(续4)
• Softmax
Softmax函数定义如下,其中Vi 是分类器前级输出单元的输出。i 表示类别索引,总的类别个数为 C。
Si 表示的是当前元素的指数与所有元素指数和的比值。通过
Softmax函数就可以将多分类的输出数值
转化为相对概率,而这些值的累和为1,常用于神经网络输出层。 表达式:
1.2
4.0
0.2
e
1.2
e
1.2
+ e
4.0
+ e
0.2
3.32
≈
3.32 +54.58 + 1.22
≈ 0.056
e
4.0
e
1.2
+ e
4.0
+ e
0.2
54.58
≈
3.32 +54.58 + 1.22
≈ 0.923
e
0.2
e
1.2
+ e
4.0
+ e
0.2
1.22
≈
3.32 +54.58 + 1.22
≈ 0.02

知
识
讲
解
小结
• 本章节介绍了深度学习一些重要的基本概念,需要理解并熟练掌握。
同时,还介绍了如何从简单的感知机逐步演化到复杂的神经网络。重
要的概念有:
ü
感知机。
接收多个输入信号,产生一个输出信号,无法解决异或问题
ü
多层感知机。
将多个感知机组合
ü
多层前馈网络。
若干个感知机组合成若干层的网络,上一层输出作为下一层输入
ü
激活函数。
将计算结果转换为输出的值,包括阶跃函数、sigmoid、tanh、ReLU





