性能度量

① 错误率与精度

错误率和精度是分类问题中常用的性能度量指标，既适用于二分类任务，也适用于多分类任务.

  • 错误率（error rate）：指分类错误的样本占样本总数的比例，即 （ 分类错误的数量 / 样本总数数量）

  • 精度（accuracy）：指分类正确的样本占样本总数的比例，即 （分类正确的数量 / 样本总数数量）

    $$精度 = 1 - 错误率$$

② 查准率、召回率与F1得分

错误率和精度虽然常用，但并不能满足所有的任务需求。例如，在一次疾病检测中，我们更关注以下两个问题：

  • 检测出感染的个体中有多少是真正病毒携带者？
  • 所有真正病毒携带者中，有多大比例被检测了出来？

类似的问题在很多分类场景下都会出现，“查准率”（precision）与“召回率”（recall）是更为适合的度量标准。对于二分类问题，可以将真实类别、预测类别组合为“真正例”（true positive）、“假正例”（false positive）、“真反例”（true negative）、“假反例”（false negative）四种情形，见下表：

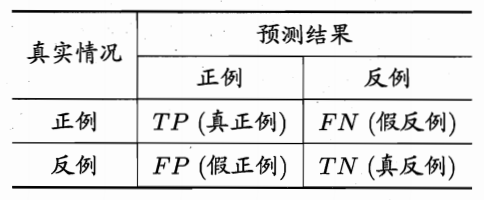
confusion_matrix

  • 样例总数：TP + FP + TN + FN

  • 查准率： TP / (TP + FP)，表示分的准不准

  • 召回率：TP / (TP + FN)，表示分的全不全，又称为“查全率”

  • F1得分：
    $$
    f1 = \frac{2 * 查准率 * 召回率}{查准率 + 召回率}
    $$

查准率和召回率是一对矛盾的度量。一般来说，查准率高时，召回率往往偏低；召回率高时，查准率往往偏低。例如，在病毒感染者检测中，若要提高查准率，只需要采取更严格的标准即可，这样会导致漏掉部分感染者，召回率就变低了；反之，放松检测标准，更多的人被检测为感染，召回率升高了，查准率又降低了. 通常只有在一些简单任务中，才能同时获得较高查准率和召回率。

查准率和召回率在不同应用中重要性也不同。例如，在商品推荐中，为了尽可能少打扰客户，更希望推荐的内容是用户感兴趣的，此时查准率更重要；而在逃犯信息检索系统中，希望让更少的逃犯漏网，此时召回率更重要。

③ 混淆矩阵

混淆矩阵也称误差矩阵，是表示精度评价的一种标准格式，用n行n列的矩阵形式来表示。每一行（数量之和）表示一个真实类别的样本，每一列（数量之和）表示一个预测类别的样本。

以下是一个预测结果准确的混淆矩阵：

A类别 B类别 C类别
A类别 5 0 0
B类别 0 6 0
C类别 0 0 7

上述表格表示的含义为：A类别实际有5个样本，B类别实际有6个样本，C类别实际有7个样本；预测结果中，预测结果为A类别的为5个，预测结果为B类别的为6个，预测结果为C类别的为7个。

以下是一个预测结果不准确的混淆矩阵：

A类别 B类别 C类别
A类别 3 1 1
B类别 0 4 2
C类别 0 0 7

上述表格表示的含义为：A类别实际有5个样本，B类别实际有6个样本，C类别实际有7个样本；预测结果中，A类别有3个样本预测准确，另外各有1个被预测成了B和C；B类别有4个预测准确，另外2个被预测成了C类别；C类别7个全部预测准确，但有1个本属于A类别、2个本属于B类别的被预测成了C类别。

根据混淆矩阵，查准率、召回率也可表示为：

查准率 = 主对角线上的值 / 该值所在列的和

召回率 = 主对角线上的值 / 该值所在行的和

④ 实验

利用sklearn提供的朴素贝叶斯分类器分类，并打印查准率、召回率、R2得分和混淆矩阵：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# 混淆矩阵示例
import numpy as np
import sklearn.model_selection as ms
import sklearn.metrics as sm
import sklearn.naive_bayes as nb

# 输入，输出
x, y = [], []

# 读取数据文件
with open("../data/multiple1.txt", "r") as f:
    for line in f.readlines():
        data = [float(substr) for substr in line.split(",")]
        x.append(data[:-1])  # 输入样本：取从第一列到导数第二列
        y.append(data[-1])  # 输出样本：取最后一列

# 样本转数组
x = np.array(x)
y = np.array(y, dtype=int)

# 划分训练集和测试集
train_x, test_x, train_y, test_y = ms.train_test_split(
    x, y, test_size=0.25, random_state=7)

# 创建高斯朴素贝叶斯分类器对象
model = nb.GaussianNB()
model.fit(train_x, train_y)  # 使用划分的训练集来训练模型
pred_test_y = model.predict(test_x)  # 预测

print("recall:", sm.recall_score(test_y,  # 真实值
                                 pred_test_y,  # 预测值
                                 average="macro"))  # 计算平均值，不考虑样本权重
print("precision:", sm.precision_score(test_y,  # 真实值
                                       pred_test_y,  # 预测值
                                       average="macro"))  # 计算平均值，不考虑样本权重
print("F1:", sm.f1_score(test_y, pred_test_y,average="macro"))

# 计算并打印模型预测的混淆矩阵
print("\n Confusion Matrix:")
cm = sm.confusion_matrix(test_y, pred_test_y)
print(cm)

打印输出：

1
2
3
4
5
6
7
8
9
recall: 0.9910714285714286
precision: 0.9903846153846154
F1: 0.9905525846702318

 Confusion Matrix:
[[22  0  0  0]
 [ 0 27  1  0]
 [ 0  0 25  0]
 [ 0  0  0 25]]

训练集与测试集

通常情况下，评估一个模型性能的好坏，将样本数据划分为两部分，一部分专门用于模型训练，这部分称为“训练集”，一部分用于对模型进行测试，这部分被称为“测试集”，训练集和测试集一般不存在重叠部分. 常用的训练集、测试集比例有：9:1, 8:2, 7:3等. 训练集和测试的划分，尽量保持均衡、随机，不能集中于某个或少量类别.

有些公共数据集在创建时，已经进行了划分. 有时候，我们需要自己对数据集进行划分，划分的方式是先打乱数据集，然后使用一种计算方法，将一部分数据划入训练集，一部分数据划入测试集.

train_test_dataset

交叉验证法

① 什么是交叉验证

在样本数量较少的情况下，如果将样本划分为训练集、测试集，可能导致单个集合样本数量更少，可以采取交叉验证法来训练和测试模型.

“交叉验证法”（cross validation）先将数据集D划分为k个大小相同（或相似）的、互不相交的子集，每个子集称为一个”折叠”（fold），每次训练，轮流使用其中的一个作为测试集、其它作为训练集. 这样，就相当于获得了k组训练集、测试集，最终的预测结果为k个测试结果的平均值.

cross_validation

② 如何实现交叉验证

sklearn中，提供了cross_val_score函数来实现交叉验证并返回评估指标值：

1
2
3
4
5
6
import sklearn.model_selection as ms

n = ms.cross_val_score(model, #模型
                       train_x, train_y,# 样本输入、输出
                       cv,  # 折叠数量
                       scoring) # 指定返回的指标

以下是关于朴素贝叶斯模型的交叉验证实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# 交叉验证示例
import numpy as np
import sklearn.model_selection as ms
import sklearn.naive_bayes as nb
import matplotlib.pyplot as mp

x, y = [], []  # 输入，输出

# 读取数据文件
with open("../data/multiple1.txt", "r") as f:
    for line in f.readlines():
        data = [float(substr) for substr in line.split(",")]
        x.append(data[:-1])  # 输入样本：取从第一列到导数第二列
        y.append(data[-1])  # 输出样本：取最后一列

train_x = np.array(x)
train_y = np.array(y, dtype=int)

# 划分训练集和测试集
#train_x, test_x, train_y, test_y = ms.train_test_split(
#    x, y, test_size=0.25, random_state=7)

# 创建高斯朴素贝叶斯分类器对象
model = nb.GaussianNB()
# 先做交叉验证，如果得分结果可以接受，再执行训练和预测
pws = ms.cross_val_score(model, x, y,
                         cv=5,  # 折叠数量
                         scoring='precision_weighted')  # 查准率
print("precision:", pws.mean())

rws = ms.cross_val_score(model, x, y, cv=5,
                         scoring='recall_weighted')  # 召回率
print("recall:", rws.mean())

f1s = ms.cross_val_score(model, x, y, cv=5,
                         scoring='f1_weighted')  # F1得分
print("f1:", f1s.mean())

acc = ms.cross_val_score(model, x, y,
                         cv=5, scoring='accuracy')  # 准确率
print("acc:", acc.mean())

执行结果：

1
2
3
4
precision: 0.996822033898305
recall: 0.9966101694915255
f1: 0.9966063988235516
acc: 0.9966101694915255