Harmonics
In the frequency domain, periodic signals have harmonic structure: they contain energy only at multiples of their fundamental frequency.
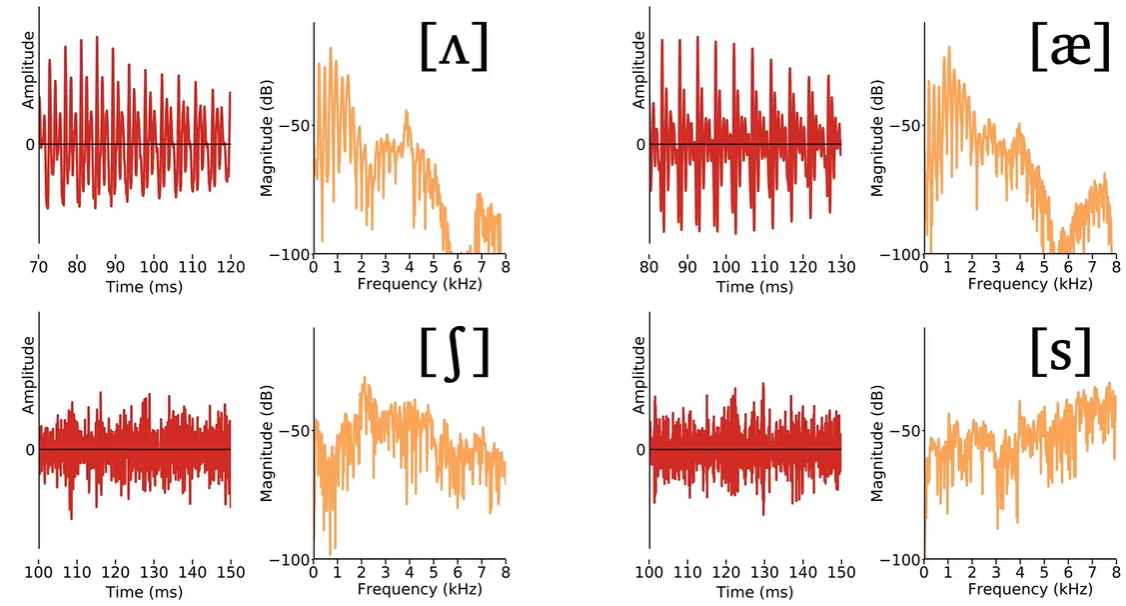
Voice sounds different from unvoiced sounds, has repeating pattern, in periodicity. So, the peak of the sound in the frequency domain is clear to observe.
Impulse train
An impulse train is the simplest periodic signal that has energy at all multiples of its fundamental frequency (and energy are evenly distributed).

Spectral envelope
Varying the shape of the spectral envelope is the primary means by which a speaker transmits a linguistic message to a listener.
Spectral envelope: The region under the curve in frequency domain.

Resonant tube
The understand how the vocal tract modifies sound, we need to start with the concept of resonance.
Q: Increased damping in a resonant system…
A: increases the bandwidth of the frequency response. Increased damping won’t increase gain (i.e., boosting of amplitude) as increased damping means the vibration of an object fades away sooner (i.e. loses amplitude), so we can rule out that answer. Bandwidth refers to the width of the frequency response curve (see M4: Vocal tract resonance and formants). A decreased bandwidth would indicate that less frequencies around the resonance frequency are boosted (and thus consume energy). This sort of narrow bandwidth is what allows a tuning fork to ring for a long time. An increased bandwidth means that more frequencies get boosted around the resonant frequency. This is associated with a lower peak amplitude (as the energy is spread across a bigger band of frequencies). This is consistent with increased damping: energy is spread over more frequencies so the oscillations due to resonance die out quicker. (M4: Vocal tract resonance and formants, Wayland Chapter 6: Damping. This is a very challenging question!)
Vocal tract resonance & formants
A speaker can vary their vocal tract shape to change its resonant frequencies, and therefore the spectral envelope of the speech they are producing.
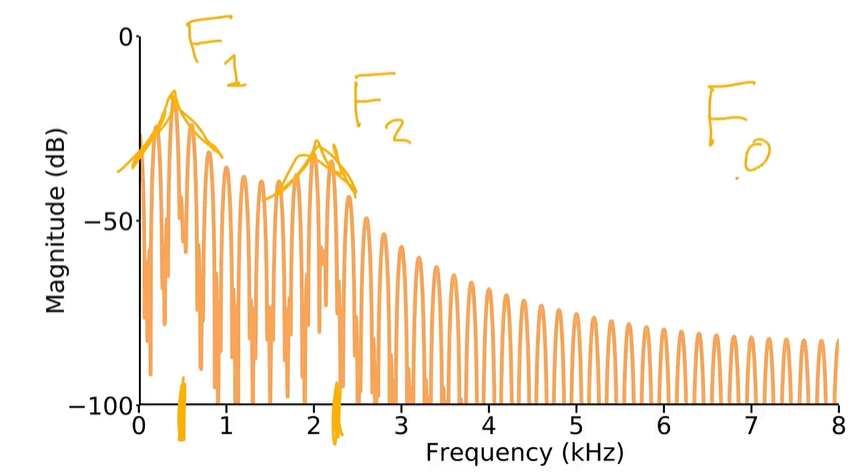
Formant frequencies: Frequencies around which acoustic energy is concentrated as a result of the filtering action of the vocal tract, visible as prominent peaks in a spectrum. (resonances of the vocal tract)
The peak is called formant, properties for the vocal tract, and $F_1$ is the first format and $F_2$ is the second formant.
But $F_0$ is is the fundamental frequency of the vocal folds, the rate of the vocal folds, not formant.
Filter
We now shift from an explicit physical model of the vocal tract as a resonating tube, to a more general model of the vocal tract as a filter operating on signals.
Filter is something map from input domain $X$ to output domain $Y$, like a function in mathematics.

Impulse response
If we want to characterise a filter in the time domain, we need to know its impulse response.
How the filter response to the impulse.
In the image below, we narrow down the analysis frame down to only one period of waveform, we have impulse response of the filter on the left, and the frequency response of the filter on the right.

Source-filter model
Finally, we arrive at a complete model of speech signals that can generate any speech sound.
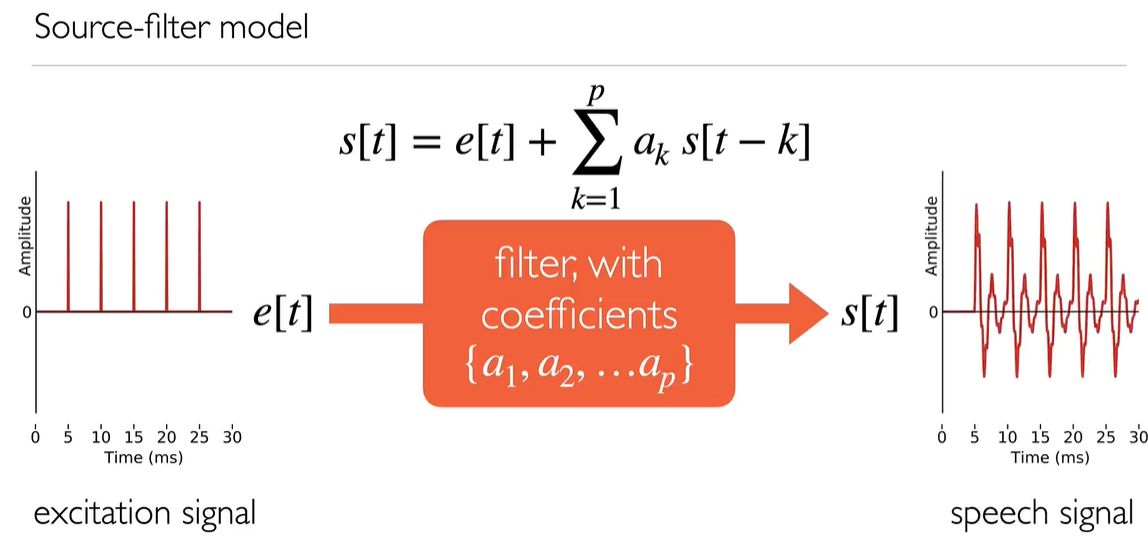
We find the impulse response/frequency response of the original sounds

Phoneme
The source-filter model brings together our understanding of speech signals, speech production, and phonetics. It can generate any speech sound: any phoneme.
Summary

Origin: Module 4 the Source-Filter Model
Translate + Edit: YangSier (Homepage)
:four_leaf_clover:碎碎念:four_leaf_clover:
Hello米娜桑,这里是英国留学中的杨丝儿。我的博客的关键词集中在编程、算法、机器人、人工智能、数学等等,点个关注吧,持续高质量输出中。
:cherry_blossom:唠嗑QQ群:兔叽的魔术工房 (942848525)
:star:B站账号:白拾Official(活跃于知识区和动画区)








