More note for this course check: Advanced-Robotics
1. 3D State Description in Robotics
1.1. Demo Case Study: 3D Navigation of a Drone in an Urban Environment
- Super Domain: Path & Motion Planning
- Type of Method: State Representation in 3D Space
1.2. Problem Definition and Variables
- Objective: To represent and track the state of a drone for 3D navigation in an urban environment.
- Variables:
- $q$: State vector including position and orientation in 3D space.
- $(x, y, z)$: 3D Cartesian coordinates for position.
- $(\phi, \theta, \psi)$: Roll, pitch, and yaw angles for orientation.
- Environmental variables: Obstacles’ positions, wind conditions, goal location.
1.3. Assumptions
- The drone operates in a three-dimensional space.
- External conditions like wind and air traffic are either known or can be sensed.
1.4. Method Specification and Workflow
- State Representation: Define $q = [x, y, z, \phi, \theta, \psi]^T$.
- 3D Environment Mapping: Utilize 3D maps or LIDAR data for environmental representation.
- Sensor Integration: Use GPS, gyroscopes, accelerometers, and LIDAR for real-time state updates.
- Advanced State Estimation: Implement algorithms like Extended Kalman Filter or SLAM (Simultaneous Localization and Mapping) for accurate state estimation in 3D.
1.5. Strengths and Limitations
- Strengths:
- Comprehensive representation of the drone’s position and orientation in 3D space.
- Facilitates complex navigation tasks, including obstacle avoidance and route optimization.
- Adaptable to a variety of 3D navigation tasks in different environments.
- Limitations:
- High computational requirements for real-time state estimation and mapping.
- Sensor accuracy and reliability can significantly affect state estimation.
- Complex environmental dynamics can challenge state representation accuracy.
1.6. Common Problems in Application
- Drift in state estimation due to sensor errors, especially in GPS-denied environments.
- Difficulty in mapping and navigating in cluttered or dynamically changing environments.
- Balancing computational load and real-time performance requirements.
1.7. Improvement Recommendations
- Integrate more robust and diverse sensors (e.g., visual odometry) to enhance state estimation.
- Employ machine learning techniques for predictive modeling of environmental dynamics.
- Optimize algorithms for efficient computation, considering the constraints of onboard processing capabilities.
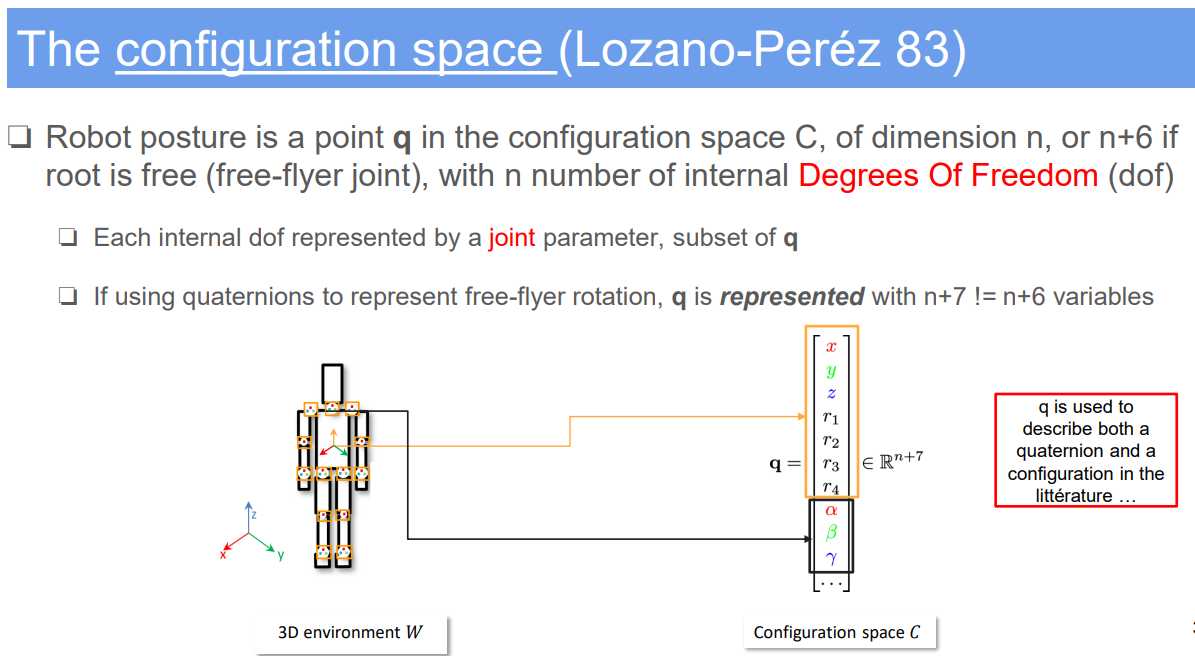
2. Euler Angles and Gimbal Lock in Robotics
2.1. Demo Case Study: Orientation Control of a Robotic Camera System
- Super Domain: Kinematics and Control Systems
- Type of Method: Orientation Representation and Control
2.2. Problem Definition and Variables
- Objective: To control the orientation of a robotic camera system using Euler angles while understanding and mitigating the risks of gimbal lock.
- Variables:
- Euler Angles $(\phi, \theta, \psi)$: Roll, pitch, and yaw angles representing the orientation of the camera.
- Gimbal Lock: A condition where two of the three gimbals align, resulting in a loss of one degree of rotational freedom.
2.3. Assumptions
- The camera system operates under a gimbal mechanism allowing three degrees of rotational freedom.
- The motion and orientation of the system can be accurately measured and controlled using Euler angles.
2.4. Method Specification and Workflow
- Euler Angle Representation: Define orientation using three rotations about principal axes.
- Sequence of rotations (e.g., Z-Y-X) is crucial for defining the orientation.
- Gimbal Lock Understanding: Recognize that gimbal lock occurs when the pitch angle ($\theta$) is at 90°, aligning two of the three rotation axes.
- Orientation Control: Implement control algorithms to adjust roll, pitch, and yaw for desired camera orientation.
- Gimbal Lock Mitigation: Monitor and manage the pitch angle to avoid approaching critical values where gimbal lock can occur.
2.5. Strengths and Limitations
- Strengths:
- Euler angles provide an intuitive way to describe orientation.
- Suitable for applications with limited rotational movement where gimbal lock can be avoided.
- Limitations:
- Gimbal lock leads to a loss of one rotational degree of freedom, making precise control impossible in certain orientations.
- Euler angles can be less intuitive for complex, three-dimensional rotational movements.
2.6. Common Problems in Application
- Unintentionally entering gimbal lock, resulting in control issues.
- Difficulty in visualizing and programming complex rotations using Euler angles.
- Accumulation of numerical and computational errors, especially near gimbal lock configurations.
2.7. Improvement Recommendations
- Implement quaternion-based representation as an alternative to avoid gimbal lock.
- Use advanced control algorithms that can detect and compensate for approaching gimbal lock conditions.
- Educate operators and programmers about the limitations and risks of gimbal lock in systems using Euler angles.

3. 3D State Description in Robotics with Quaternion Improvement
3.1. Demo Case Study: Advanced 3D Navigation of an Aerial Robot in Complex Environments
- Super Domain: Path & Motion Planning
- Type of Method: Enhanced State Representation in 3D Space
3.2. Problem Definition and Variables
- Objective: To accurately represent and manage the 3D state of an aerial robot for complex navigation tasks.
- Variables:
- $q$: Enhanced state vector including position and orientation in 3D space.
- $(x, y, z)$: 3D Cartesian coordinates for position.
- Quaternion $(q_w, q_x, q_y, q_z)$: Representing orientation to overcome Euler angle limitations.
3.3. Assumptions
- The robot operates in a dynamic, three-dimensional environment.
- High accuracy in orientation representation is crucial for navigation and task execution.
3.4. Method Specification and Workflow
- State Representation: Define $q = [x, y, z, q_w, q_x, q_y, q_z]^T$.
- Quaternion Usage: Replace Euler angles with quaternions to avoid issues like gimbal lock and provide more accurate and stable orientation representation.
- Sensor Fusion: Integrate IMU data with visual odometry and LIDAR for robust state estimation.
- Advanced Algorithms: Use state-of-the-art algorithms like Unscented Kalman Filter or SLAM for precise state tracking in 3D space.
3.5. Strengths and Limitations
- Strengths:
- Quaternions provide a more robust and singularity-free representation of orientation in 3D space.
- Enhanced precision in orientation helps in complex maneuvers and accurate navigation.
- Suitable for high-dynamic environments like aerial robotics in urban or natural terrains.
- Limitations:
- Increased complexity in understanding and implementing quaternion mathematics.
- Higher computational demands for real-time quaternion-based state estimation.
- Requires sophisticated sensor fusion techniques to fully leverage quaternion advantages.
3.6. Common Problems in Application
- Complexity in translating quaternion operations into practical control commands.
- Challenges in seamlessly integrating quaternion data with traditional position sensors.
- Ensuring numerical stability and avoiding normalization issues with quaternions.
3.7. Improvement Recommendations
- Integrate machine learning to predict and compensate for environmental dynamics and sensor inaccuracies.
- Develop specialized algorithms for efficient quaternion normalization and operation.
- Utilize hardware acceleration for real-time processing of complex quaternion-based calculations.

4. Special groups for rotations

5. Displacement in Robotics (Translation and Rotation)
5.1. Demo Case Study: Precise Manipulator Movement in Industrial Robotics
- Super Domain: Kinematics
- Type of Method: Geometric and Kinematic Analysis
5.2. Problem Definition and Variables
- Objective: To accurately describe and control the displacement of a robotic manipulator, including both translation and rotation.
- Variables:
- $\mathbf{p}$: Position vector representing translation in Cartesian coordinates $(x, y, z)$.
- Rotation: Represented by Euler angles $(\phi, \theta, \psi)$, rotation matrices, or quaternions.
5.3. Assumptions
- The manipulator operates within a rigid body framework.
- Joint movements are precise and can be accurately measured.
5.4. Method Specification and Workflow
- Translation: Described by linear displacement along x, y, and z axes.
- Formula: $\Delta \mathbf{p} = \mathbf{p}{final} - \mathbf{p}{initial}$.
- Rotation:
- Euler Angles: Changes in orientation described by roll ($\phi$), pitch ($\theta$), and yaw ($\psi$).
- Rotation Matrix: $\mathbf{R} = \mathbf{R}_z(\psi) \mathbf{R}_y(\theta) \mathbf{R}_x(\phi)$.
- Quaternion: $q = [q_w, q_x, q_y, q_z]$, providing a singularity-free representation.
- Homogeneous Transformation Matrix: Combines translation and rotation in a single matrix.
- Formula: $\mathbf{T} = \begin{bmatrix} \mathbf{R} & \mathbf{p} \ \mathbf{0} & 1 \end{bmatrix}$.
5.5. Strengths and Limitations
- Strengths:
- Provides a comprehensive way to describe both position and orientation.
- Suitable for a wide range of robotic applications, including automation and assembly.
- Facilitates the calculation of kinematic chains and motion planning.
- Limitations:
- Complexity in calculations, especially for rotations in 3D space.
- Euler angles can suffer from gimbal lock in certain configurations.
- Precision depends on the accuracy of the measurement systems.
5.6. Common Problems in Application
- Accumulation of numerical errors in successive transformations.
- Complexity in inverse kinematics for determining joint angles from desired end-effector position.
- Difficulty in intuitively understanding and visualizing quaternion-based rotations.
5.7. Improvement Recommendations
- Implement advanced computational tools for handling complex kinematic calculations.
- Utilize quaternions for rotation to avoid gimbal lock and improve computational efficiency.
- Integrate feedback systems for error correction in real-time motion control.

Reference: The University of Edinburgh, Advanced Robotics, course link
Author: YangSier (discover304.top)
🍀碎碎念🍀
Hello米娜桑,这里是英国留学中的杨丝儿。我的博客的关键词集中在编程、算法、机器人、人工智能、数学等等,持续高质量输出中。
🌸唠嗑QQ群:兔叽の魔术工房 (942848525)
⭐B站账号:白拾Official(活跃于知识区和动画区)
Cover image credit to AI generator.









