🔥人工智能
笔记和资料,涉及到深度学习、自动驾驶等领域。

🔥机器人
包括ROS机器人框架笔记。Beginer Friendly

✅Python教程
从0到1,在深入人工智能的全套Python笔记。

❤️经验经历
过往的感悟和思考。发病日记。

✨碎片技术
学习工作中遇到的很赞的技术碎片,整理好了。

✨学习积累
相对于碎片技术的,已经沉淀为自己的资本的内容。
PMR Introduction & Assumptions for Efficient Representation
1. Course Structure
Assumptions with reasons and learning/reasoning.
Half half.
2. Basic Assumptions for Efficient Model Representation
Independence: limit the number of interaction.
Interaction: restrict the way things interact with each other.
2.1. Independence
2.2. Interaction
3. Additional Material
3.1. Sensitivityu and Specificity
Sensitivity: True Positive
Specificity: True Negtive
Simply another way saying the same thing.
敏感性(Sensitivity)与特异性(Specificity)
3.2. Bayes’ rule
$ ...
NLU Introduction
1. Natural Language Understanding
Broadly: any computational problem where the input is natural language, and the output is structured information that a computer can store (e.g. in a database) or execute (e.g. a command to a digital assistant).
1.1. Digital Assistants
1.2. Question answering
1.3. Sentiment analysis
1.4. Syntactic parsing
1.5. Semantic parsing
2. Natural Language Generation
Broadly: any computational problem where the input is non-linguistic data (e.g. data, images, sound) ...
ARO Robot Geometry
More note for this course check: Advanced-Robotics
1. 3D State Description in Robotics
1.1. Demo Case Study: 3D Navigation of a Drone in an Urban Environment
Super Domain: Path & Motion Planning
Type of Method: State Representation in 3D Space
1.2. Problem Definition and Variables
Objective: To represent and track the state of a drone for 3D navigation in an urban environment.
Variables:
$q$: State vector including position and orientation in 3D space.
$(x, y, z)$: 3D Cartesian coordin ...
【七牛云】Enhanced Workflow for Managing Files in Qiniu Cloud Storage
English Version中文版本Step 1: Listing Bucket Contents (Helper Function)
Before restoring files, it’s beneficial to list the contents of the bucket to identify the files to be restored.
Command
1.\qshell.exe listbucket2 <bucket-name> --file-types 2,3 --show-fields Key,FileType
Explanation
Purpose: Lists the contents of a specified bucket.
Parameters:
<bucket-name>: Replace with the name of your bucket.
--file-types 2,3: Specifies the types of files to list.
--show-fields Key,FileType: ...
【模板】Hexo Docker Nginx 个人博客服务器部署
🤖 TLDR By ChatGPT
本指南提供了在服务器上设置Git仓库、将本地Hexo页面推送到服务器仓库、在服务器上创建Nginx配置文件以及在服务器上运行Nginx容器的方法。
在服务器上的指定路径下运行git init初始化Git仓库。
参考Easy Hexo指南,使用提供的配置将本地Hexo页面推送到服务器仓库。
提供的配置在服务器上创建Nginx配置文件,包括MIME类型、日志、SSL和HTTP和HTTPS的服务器块。
使用官方Docker镜像在服务器上运行Nginx容器。使用docker pull nginx拉取镜像,然后使用提供的命令运行容器。
请确保用适当的值替换所有<todo: comment>占位符。
There are several <todo: comment> need to be replaced.
✨Initialise git repository on server
123cd <todo: the path for repository>git init
✨Push local hexo pages t ...
【编程】R: Getting Into Project of R
:star: what is an r project include in r studio?
An R project in RStudio is a self-contained directory that contains all the files and resources associated with a specific R project. This includes the R code files, data files, output files, and any additional packages or libraries needed for the project. RStudio automatically creates a new R project for each project you start, and allows you to easily switch between different projects within the RStudio interface. R projects in RStudio also prov ...
PI Week2 Responsibility
More note for this course check: Professional Issues
Responsibility
Definition
Responsibility is an assigning of roles by some larger section of society.
Explanation
We are talking about responsibility as the degree to which individuals or groups are accountable for actions, events, or other changes in the world.
This might mean attributing a certain amount of praise or blame to those agents for those actions.
But also it means attributing an imperative to them that they should be thinking ...
SP Module 0 – Getting Started
More note for this course check: Speech-Processing
Test to Speech Synthesis TTS
the generation of speech from text input
Automatic Speech Recognition ASR
the transcription of speech into text
Key ideas
PHON – phonetics and phonology
SIGNALS – signal processing, with a focus on speech signals
TTS – text-to-speech synthesis
ASR – automatic speech recognition
SKILLS – maths, computing, writing
The phonetics modules in this course are intended to complement the speech processing content. ...
PAR Group PLANING BOOK
Project Name: GO PRO BRO
Planning Book Version: v0.1
Background
Today, undergraduate students are looking for opportunities to gain the experience of research. But some of them may head to the public, and start a summer school, which is too expensive for undergraduate students, and not fair for those suffer in poverty. Besides, things like summer school is for student in high or middle school who have a strong willing to start their research career but don’t have someone can help or teach them ...
MOB LEC1 Introduction
More note for this course check: Introduction-to-Mobile-Robotics
Meaning of robot
Origin of the Term: The word “robot” was introduced to the public by Czech (捷克共和国) writer Karel Čapek (卡雷尔·恰佩克) in his science-fiction play R.U.R. (Rossum’s Universal Robots) in 1920. In Czech language, “robota” means “labour” or “work”.
Original purpose of robots: automatic/autonomous labour that frees humans from tedious jobs
Use cases of robot
People fear
Dangerous: exploration, chemical spill cleanup, d ...
【指导】科研工作团队协作避坑指南
本文站在第三方的角度审视我在2022年的团队科研经历,一来是自省,二来是帮助更多同学更好的开始自己的科研生活。
科研工作是围绕一个科学问题展开的探索,只要是探索就有成功,有失败。而人工智能的科研探索,永远是以失败为主旋律。再详尽的计划,再强大的开发能力,都无法保证实验不出现问题。和数学条理清晰的证明不一样,人工智能深度学习的黑盒性质,使科研工作的展开注定磕磕绊绊。
:star:对科研成果的要求
不同会议或期刊的收录倾向不同,例如CVPR喜欢新应用,NeurlPS喜欢理论的突破,AAAI相对就比较杂食,但对于一篇好文章的要求无非如下:
研究点新颖,要做到读者听上去就想要复现一下。
背景资料详实,需要找老前辈讨论。
论证的严谨,参考文献充足且逻辑自洽。
实验完备且充分,多角度多任务多场景(多数据集、多网络适配、多应用)
文章的行文规范且流畅,体现一个团队的积累。
:star:研究的三个板块
对于一个课题组,如何进行人员的组织是一定要考虑的问题。任何一个错误的分工,或者一个模糊不清的角色定位都会造成课题推进的困难。接下来我们从三个主要的板块,展开讨论,科研团队中的大家如何扮演好自己 ...
【指导】Mendeley文献管理工具教程
:star:为什么需要文献管理工具?
作为一名热爱学术的研究生,每天要阅读许多篇论文,每篇论文要经历繁琐的检索、下载、阅读的过程;在读了许多文献之后,想去回顾一下以前读过的文章,却发现面对着电脑中各种文献的文件夹,怎么也找不到想要找的文章了。这时候就需要一个文献管理工具,管理你的成千上百的文献,让你在写论文时很顺手地找到想要的文献。
:star:为什么选用Mendeley?
:star:Mendeley的下载
Mendeley有两个版本,官方页面上的是Mendeley Manager,但是异常难用。这里建议使用Mendeley Desktop配置本地论文仓库,也可以通过设置云端同步实现跨平台。
:star:Mendeley的基本使用
:stars:使用界面
:stars:【重点】配置本地仓库
:stars:配置云端同步
注:不推荐使用云端同步,第一Mendeley的空间有限,第二没有必要。如有需要,可以尝试Mendeley的第三方云端仓库同步。
:stars:Mendeley汉化
可以直接下载绿色网传中文版,暂时没找到汉化补丁。
:star:Mendeley常用功能
:st ...
【星光03】GPU多卡排队/抢占/贪心脚本,实验室必备
经常有小伙伴和我抱怨说拿不到计算资源,于是这不就来了吗。这是一个后台GPU排队脚本,主要是为了解决实验室中的显卡使用/占用问题。
✨阅前须知
Talk is cheap, show me the code. 废话少说,直接给我代码!
脚本代码跳转链接:脚本在这里
说给小白白的一些话:
本文只针对Nvidia显卡,依赖nvidia-smi查看显卡状态的命令。
本文提出的方法使用的是python作为终端脚本的启动器,默认python即可。
本文的方法是多显卡的贪心脚本,一个空窗期内有几张显卡就会用几张,小心使用。
本文方法无法实现显卡累加的操作,如果你想要那种闲下一张卡就抢过来的脚本,可以试试在本文的基础上进行修改。
✨预备知识
对理解GPU多卡排队脚本有帮助的内容:
在服务器上训练人工智能模型的时候往往是启动一个后台任务,启动后台任务的方法如下: 12#!/bin/bashnohup 【命令】 &
对于使用GPU的后台任务,如果没有好好的退出,会一直占用GPU资源。所以需要执行如下命令退出: 123456# 执行以下命令在全部线程中寻找你的后台线程:ps -ef | ...
论文咋水
论文和自己的笔记不一样,和我成天写的博客类似,都是要提供最多的相关信息,便于读者理解。
只要有给小白讲明白这个点的想法,就不愁没得写
而且大概率会超页数。超了删,好删;少了加,就难喽
至少比你低一两个年级的同学能看懂或者不是很了解天体物理的量子物理教授能看懂
水论文小技巧1:谷歌翻译,中英或者英法互译,来回译上几轮,字数就多了
水论文小技巧2:分析文章观点展开逻辑,力求每一个观点的逻辑展开流程一致。之后只要多一环逻辑,全文每一块都可以多这一环
水论文小技巧3:大量公式,表格,图片
水论文小技巧4:观点前置,最后重复观点,强调重点
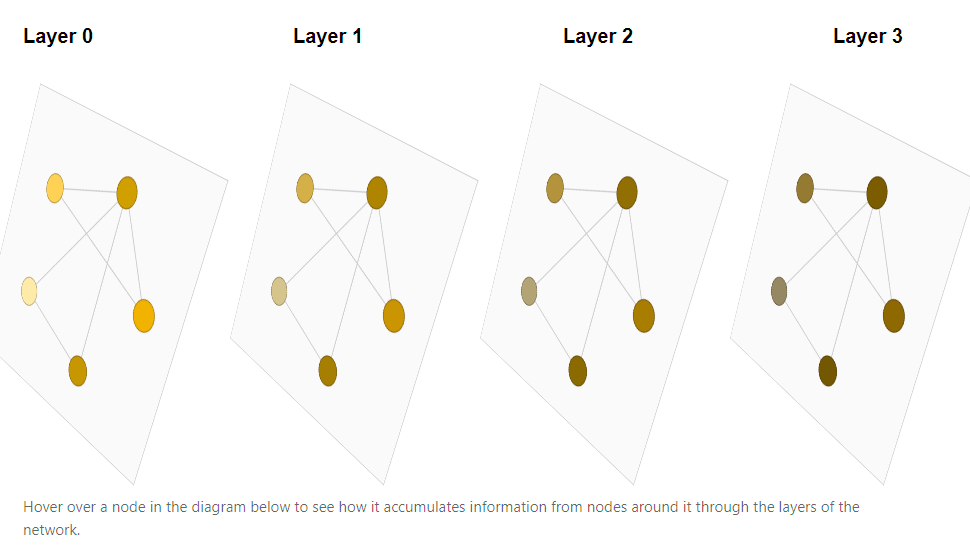
GNN Recap
A Gentle Introduction to Graph Neural Networks
为什么使用GNN,因为相关性是一个网络。
邻接矩阵是GNN要得到的东西,但是相关性的邻接矩阵不就是相关性矩阵吗
所以可以直接计算相关性矩阵来实现,但是这种做法是十分耗时的。
而且也只能是起到attention的作用,增强了某些信息。
通过增加空白节点作为胶水的形式,融合模态。
思考:预训练编码器(信源编码),然后通过任意DNN预测模态间特征的邻接矩阵(融合指导),使用GNN预测每一个特征上的附加信息(信道编码)。
注:附加信息量与初始信息量的比例,等于多个模态编码后的码长之比。